Elliptical Cylinder Calculator
Calculator and formulas for calculating an elliptical cylinder
Elliptical Cylinder Calculator
The Elliptical Cylinder
The elliptical cylinder is a cylinder with an elliptical base.
Elliptical Cylinder Properties
The Elliptical Cylinder: Cylinder with elliptical base
Elliptical Cylinder Visualization
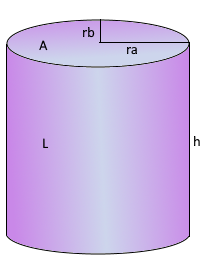
Elliptical Cylinder
Cylinder with elliptical base
Parameters
a: Major semi-axis of the ellipse
b: Minor semi-axis of the ellipse
h: Height of the cylinder
Elliptical base with height.
Two different radii a and b.
|
|
What is an Elliptical Cylinder?
The elliptical cylinder is an important geometric body:
- Definition: Cylinder with elliptical rather than circular base
- Parameters: Two semi-axes a and b of the ellipse plus height h
- Properties: Prismatic body with constant cross-sectional area
- Special case: When a = b, it becomes a circular cylinder
- Applications: Mechanical engineering, architecture, container technology
- Mathematics: Ramanujan approximation for ellipse perimeter
Geometric Properties of the Elliptical Cylinder
The elliptical cylinder shows characteristic geometric properties:
Basic Parameters
- Semi-axis a: Major semi-axis of the elliptical base
- Semi-axis b: Minor semi-axis of the elliptical base
- Height h: Distance between the two bases
- Eccentricity: Ratio e = √(1-b²/a²)
Special Properties
- Prismatic: Constant cross-sectional area over height
- Symmetry: Two axes of symmetry in the base
- Perimeter: Exact calculation only via elliptic integrals
- Ramanujan formula: Approximation with error < 0.04%
Mathematical Relationships of the Elliptical Cylinder
The elliptical cylinder follows elegant mathematical laws:
Volume Formula
Volume is the product of ellipse area and height. Simple and elegant.
Perimeter Formula (Ramanujan)
Ramanujan approximation with maximum deviation of 0.04%. Practically exact for all applications.
Applications of the Elliptical Cylinder
Elliptical cylinders find applications in various fields:
Mechanical Engineering & Technology
- Elliptical containers and tanks
- Pipes with oval cross-section
- Pneumatic cylinders
- Machine components
Architecture & Construction
- Elliptical columns
- Tunnels with oval cross-section
- Bridge elements
- Modern building architecture
Science & Technology
- Pressure chambers and reactors
- Fluid mechanics
- Medical technology
- Optical systems
Automotive Technology
- Fuel tanks
- Exhaust systems
- Hydraulic cylinders
- Aerodynamic components
Formulas for the Elliptical Cylinder
Volume (V)
Volume of the elliptical cylinder
Base Area (A)
Area of the elliptical base
Lateral Area (L)
Lateral surface of the cylinder
Surface Area (S)
Total surface area of the cylinder
Perimeter (P) - Ramanujan Approximation
\[\text{where } \lambda = \frac{a-b}{a+b}\]
Ramanujan approximation for ellipse perimeter with maximum error of 0.04%. This formula is practically exact for all technical applications.
Calculation Example for an Elliptical Cylinder
Given
Find: All parameters of the elliptical cylinder
1. Base Area Calculation
For a = 5 cm, b = 4 cm:
\[A = \pi \cdot a \cdot b\] \[A = \pi \cdot 5 \cdot 4\] \[A = 20\pi ≈ 62.83 \text{ cm}^2\]The elliptical base area is approximately 62.83 cm²
2. Volume Calculation
With A = 62.83 cm², h = 10 cm:
\[V = A \cdot h = \pi \cdot a \cdot b \cdot h\] \[V = 20\pi \cdot 10\] \[V = 200\pi ≈ 628.32 \text{ cm}^3\]The volume is approximately 628.32 cm³
3. Perimeter Calculation (Ramanujan)
Ramanujan parameters:
\[\lambda = \frac{5-4}{5+4} = \frac{1}{9} ≈ 0.111\] \[\lambda^2 ≈ 0.0123\] \[P ≈ \pi \cdot 9 \cdot \left(1+\frac{3 \cdot 0.0123}{10+\sqrt{4-3 \cdot 0.0123}}\right)\] \[P ≈ 28.38 \text{ cm}\]The perimeter is approximately 28.38 cm
4. Surface Area Calculation
Lateral area and total surface area:
\[L = P \cdot h = 28.38 \cdot 10 ≈ 283.8 \text{ cm}^2\] \[S = 2A + L = 2 \cdot 62.83 + 283.8\] \[S ≈ 409.46 \text{ cm}^2\]The total surface area is approximately 409.46 cm²
5. Summary
The elliptical cylinder with all characteristic parameters
6. Comparison with Circular Cylinder
a=5, b=4, h=10
V≈628.32 cm³
r=4.5, h=10
V≈636.17 cm³
r = √(a·b) ≈ 4.47
≈ 98.8% of circle
The elliptical cylinder has approximately the same volume as a circular cylinder with radius √(a·b)
The Elliptical Cylinder: Elegance of the Ellipse in Three Dimensions
The elliptical cylinder is a fascinating geometric body that extends the elegance of the ellipse into the third dimension. As a generalization of the classical circular cylinder, it offers increased flexibility for technical and architectural applications through its two different semi-axes. The mathematical beauty lies in the combination of the simple volume formula with the more complex, yet precise Ramanujan approximation for the ellipse perimeter, which delivers practically exact results.
The Geometry of the Ellipse
The elliptical cylinder shows the perfection of elliptical geometry:
- Elliptical base: Two different semi-axes a and b define the basic shape
- Prismatic structure: Constant cross-sectional area over the entire height
- Axes of symmetry: Two orthogonal axes of symmetry in the base
- Eccentricity: Measure of deviation from circular form
- Ramanujan precision: Approximation formula with error < 0.04%
- Special case circle: When a = b, it becomes the classical circular cylinder
- Practical flexibility: Adaptation to various spatial conditions
Versatile Applications
Technical Superiority
In technology, elliptical cylinders enable optimized pressure distribution and material utilization in tanks and containers.
Architectural Elegance
In architecture, elliptical columns and structures create harmonious proportions and efficient space utilization.
Flow Optimization
Elliptical profiles reduce flow resistance and optimize aerodynamics in automotive technology and aviation.
Mathematical Beauty
The combination of simple volume formula and precise perimeter approximation shows the elegance of applied mathematics.
Summary
The elliptical cylinder embodies the perfect balance between geometric elegance and practical applicability. Its elliptical base defined by two semi-axes, extended into the third dimension of height, makes it a versatile and efficient geometric body. The simple volume formula V = π·a·b·h and the precise Ramanujan approximation for the perimeter show how mathematical elegance and practical utility harmonize. From optimized pressure vessels to aerodynamic components to architectural masterpieces - the elliptical cylinder connects the beauty of the ellipse with the functionality of the third dimension and proves that geometry can be both aesthetically appealing and technically superior.