Hollow Cylinder Calculator
Calculator and formulas for calculating a hollow cylinder
Hollow Cylinder Calculator
The Hollow Cylinder
The hollow cylinder is a hollow circular cylinder with outer and inner radius.
Hollow Cylinder Properties
The Hollow Cylinder: Hollow circular cylinder with outer and inner radius
Hollow Cylinder Visualization
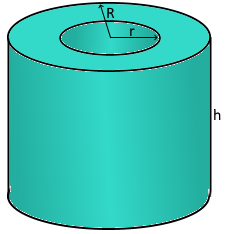
Hollow Cylinder
Tubular body with hollow space
Components
R: Outer radius (external boundary)
r: Inner radius (hollow space)
h: Height of the cylinder
Hollow circular cylinder.
Material savings through hollow space.
|
|
What is a Hollow Cylinder?
The hollow cylinder is an important geometric body:
- Definition: Hollow cylinder with circular cross-section and central hollow space
- Parameters: Outer radius R, inner radius r, and height h
- Properties: Tubular body with constant wall thickness
- Wall thickness: t = R - r (difference of radii)
- Applications: Pipes, tubes, columns, containers
- Mathematics: Difference of two cylinders (R² - r²)
Geometric Properties of the Hollow Cylinder
The hollow cylinder shows characteristic geometric properties:
Basic Parameters
- Outer radius R: Radius of the external boundary
- Inner radius r: Radius of the central hollow space
- Height h: Distance between the annular surfaces
- Wall thickness t: t = R - r (material thickness)
Special Properties
- Four surfaces: 2 annular surfaces + outer + inner lateral surface
- Rotational symmetry: Symmetry around the central axis
- Material savings: Hollow space reduces material consumption
- Structural efficiency: High stability with low weight
Mathematical Relationships of the Hollow Cylinder
The hollow cylinder follows elegant mathematical laws:
Volume Formula
The volume is the difference of two cylinders. Elegant subtraction.
Surface Area Formula
Combination of annular surfaces and both lateral surfaces (inner and outer).
Applications of the Hollow Cylinder
Hollow cylinders find applications in various fields:
Piping Technology
- Water pipes and sewage pipes
- Gas lines and steam pipes
- Hydraulic and pneumatic lines
- Chemical process pipes
Construction & Architecture
- Hollow support columns
- Cable ducts and conduits
- Ventilation shafts
- Architectural elements
Mechanical Engineering & Automotive
- Cylinder sleeves and bushings
- Exhaust pipes and mufflers
- Hydraulic cylinders
- Bearing and guide bushings
Process Engineering
- Reaction tubes
- Heat exchangers
- Distillation columns
- Bioreactor vessels
Formulas for the Hollow Cylinder
Volume (V)
Volume as difference between outer and inner cylinder
Base Area (A)
Annular area of the base surface
Lateral Areas (L)
Sum of outer and inner lateral surface
Total Surface Area (S)
Two annular surfaces plus lateral surfaces
Individual Lateral Surfaces
\[L_o = 2\pi Rh\]
\[L_i = 2\pi rh\]
\[t = R - r\]
The hollow cylinder consists of four different surface parts
Inverse Formulas
\[h = \frac{V}{\pi(R^2-r^2)}\]
\[P = 2\pi r\]
Useful inverse formulas for practice
Calculation Example for a Hollow Cylinder
Given
Find: All parameters of the hollow cylinder
1. Volume Calculation
For R = 5 cm, r = 4 cm, h = 10 cm:
\[V = \pi \cdot (R^2 - r^2) \cdot h\] \[V = \pi \cdot (5^2 - 4^2) \cdot 10\] \[V = \pi \cdot (25 - 16) \cdot 10\] \[V = 90\pi ≈ 282.74 \text{ cm}^3\]The volume is approximately 282.74 cm³
2. Base Area Calculation
Annular area (one base):
\[A = \pi \cdot (R^2 - r^2)\] \[A = \pi \cdot (25 - 16)\] \[A = 9\pi ≈ 28.27 \text{ cm}^2\]One annular area is approximately 28.27 cm²
3. Lateral Areas Calculation
Individual lateral surfaces:
\[L_o = 2\pi \cdot 5 \cdot 10 = 100\pi ≈ 314.16 \text{ cm}^2\] \[L_i = 2\pi \cdot 4 \cdot 10 = 80\pi ≈ 251.33 \text{ cm}^2\] \[L = L_o + L_i ≈ 565.49 \text{ cm}^2\]The total lateral surfaces are approximately 565.49 cm²
4. Total Surface Area
All surfaces combined:
\[S = 2A + L\] \[S = 2 \cdot 28.27 + 565.49\] \[S = 56.54 + 565.49\] \[S ≈ 622.03 \text{ cm}^2\]The total surface area is approximately 622.03 cm²
5. Additional Parameters
t = R - r = 1 cm
P = 2πr ≈ 25.13 cm
Po = 2πR ≈ 31.42 cm
rm = (R+r)/2 = 4.5 cm
Additional useful parameters of the hollow cylinder
6. Summary
The hollow cylinder with all characteristic parameters
7. Practical Example: Water Pipe
V ≈ 282.74 cm³
≈ 0.28 liters
S ≈ 622.03 cm²
Pipe surface area
Cross-section: 28.27 cm²
For flow calculations
A water pipe with these dimensions holds about 0.28 liters per 10 cm length
8. Comparison with Solid Cylinder
R=5, r=4, h=10
V≈282.74 cm³
r=5, h=10
V≈785.40 cm³
≈ 64% less volume
More efficient!
The hollow cylinder saves about 64% material compared to a solid cylinder of the same outer dimensions
The Hollow Cylinder: Perfection of Material Efficiency
The hollow cylinder is a fascinating geometric body that embodies the perfect balance between structural stability and material efficiency. As a hollow circular cylinder with centrally removed volume, it offers maximum functionality with minimal material usage. This unique property makes it one of the most important and versatile geometric bodies in engineering, architecture, and mechanical engineering, where weight savings and cost efficiency are crucial.
The Geometry of Efficiency
The hollow cylinder shows the perfection of structural optimization:
- Double radii: Outer radius R and inner radius r define the form
- Material savings: Central hollow space reduces material consumption
- Structural efficiency: High stability with low weight
- Four surfaces: Outer and inner lateral surface plus two annular surfaces
- Wall thickness t = R - r: Defines the material thickness
- Rotational symmetry: Perfect symmetry around the central axis
- Versatile application: From piping to architecture
Technical Superiority
Piping Technology
As the basic form of all pipelines, the hollow cylinder enables efficient transport of liquids, gases, and other media with optimal material utilization.
Structural Lightweight Construction
In architecture and construction, hollow supports and columns offer maximum load-bearing capacity with minimal dead weight and material consumption.
Mechanical Engineering Innovation
Cylinder sleeves, guide bushings, and bearing bushings use the precise geometry for optimal function with reduced material requirements.
Process Engineering Perfection
Reaction tubes and heat exchangers maximize the surface-to-volume ratio for optimal heat and mass transfer.
Summary
The hollow cylinder embodies the perfect synthesis of geometric elegance and technical efficiency. Its form, characterized by the central hollow space and described by the elegant difference formula π(R²-r²)h, makes it the epitome of intelligent material usage. The combination of structural stability, weight savings, and versatile applicability shows how mathematical precision and practical necessity harmonize. From vital water pipes to load-bearing architectural elements to precise machine components - the hollow cylinder proves that less is often more and demonstrates how the art of omission leads to maximum functionality. It is geometric proof that efficiency and elegance are inseparably connected.