Bicylinder Calculator
Calculator and formulas for calculating a bicylinder (Steinmetz solid)
Bicylinder Calculator
The Bicylinder
The bicylinder is a Steinmetz solid created by the intersection of two orthogonal circular cylinders.
Bicylinder Properties
The Steinmetz Solid: Intersection volume of two orthogonal circular cylinders
Bicylinder Visualization
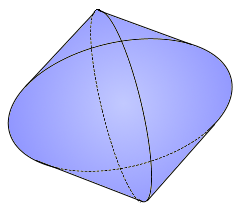
Bicylinder View
Steinmetz solid from two cylinders

Construction of a Bicylinder
Formation through cylinder intersection
Van helsing, CC BY-SA 3.0, via Wikimedia Commons
Classic Steinmetz solid.
Two orthogonal circular cylinders.
|
|
What is a Bicylinder?
The bicylinder (Steinmetz solid) is a fundamental geometric body:
- Definition: Intersection volume of two orthogonal circular cylinders with equal radius
- Name: Named after the German mathematician Jakob Steiner
- Properties: Highly symmetric body with 6 identical surfaces
- Construction: Two cylinders intersect perpendicularly
- Applications: Architecture, mechanical engineering, crystallography
- Mathematics: Simple formulas with factor 16
Geometric Properties of the Bicylinder
The bicylinder shows remarkable geometric properties:
Basic Parameters
- Radius r: Uniform radius of both cylinders
- Orthogonality: Cylinder axes are perpendicular to each other
- Intersection axes: Both axes intersect at the origin
- Symmetry: 3-fold rotational symmetry around each axis
Special Properties
- 6 identical surfaces: Each surface is a curved surface
- Edge length: All 12 edges have length 2r
- Mirror axes: 9 mirror planes
- Convexity: Completely convex body
Mathematical Relationships of the Bicylinder
The bicylinder follows elegant mathematical laws:
Volume Formula
The volume is 16/3 times the cube of the radius. Elegant and easy to remember.
Surface Formula
The surface area is 16 times the square of the radius. Simple linear relationship.
Applications of the Bicylinder
Bicylinders find applications in various fields:
Architecture & Construction
- Column connections
- Dome constructions
- Intersection structures
- Sculptural elements
Mechanical Engineering & Technology
- Pipe connections
- Joint parts
- Machine elements
- 3D printed objects
Science & Research
- Crystallography
- Materials science
- Geometric studies
- Topology
Art & Design
- Sculptural works
- Furniture design
- Jewelry design
- Industrial design
Formulas for the Bicylinder
Volume (V)
Volume of the bicylinder as a function of radius
Surface Area (S)
Total surface area of the bicylinder
Radius from Volume
Radius calculated from volume
Radius from Surface Area
Radius calculated from surface area
Bicylinder Properties
All formulas contain 16
Highly symmetric body
12 edges of length 2r
6 identical surfaces
The bicylinder is a mathematically elegant and symmetric body
Calculation Example for a Bicylinder
Given
Find: Volume and surface area of the bicylinder
1. Volume Calculation
For r = 5 cm:
\[V = \frac{16}{3} \cdot r^3\] \[V = \frac{16}{3} \cdot 5^3\] \[V = \frac{16}{3} \cdot 125\] \[V = \frac{2000}{3} ≈ 666.67 \text{ cm}^3\]The volume is approximately 666.67 cm³
2. Surface Area Calculation
For r = 5 cm:
\[S = 16 \cdot r^2\] \[S = 16 \cdot 5^2\] \[S = 16 \cdot 25\] \[S = 400 \text{ cm}^2\]The surface area is 400 cm²
3. Comparison with Sphere
Sphere with same radius:
\[V_{Sphere} = \frac{4}{3}\pi r^3 ≈ 523.6 \text{ cm}^3\] \[S_{Sphere} = 4\pi r^2 ≈ 314.2 \text{ cm}^2\]
Ratio:
V_Bicylinder / V_Sphere ≈ 1.27
S_Bicylinder / S_Sphere ≈ 1.27
The bicylinder is about 27% larger than the sphere
4. Verification Check
Check from volume:
\[r = \sqrt[3]{\frac{3 \cdot 666.67}{16}}\] \[r = \sqrt[3]{\frac{2000}{16}} = \sqrt[3]{125} = 5 \text{ cm}\]Check from surface area:
\[r = \sqrt{\frac{400}{16}} = \sqrt{25} = 5 \text{ cm}\]Both calculations confirm r = 5 cm
5. Summary
The classic bicylinder with all characteristic properties
The Bicylinder: Elegance of Symmetry
The bicylinder is a fascinating geometric body that embodies the elegance of symmetry and the beauty of geometry. As a Steinmetz solid, named after the German mathematician Jakob Steiner, it is created by the intersection of two orthogonal circular cylinders of equal radius. This simple construction leads to a highly symmetric body with remarkable mathematical properties and practical applications in architecture, mechanical engineering, and art.
The Geometry of Orthogonality
The bicylinder shows the perfection of orthogonal intersections:
- Orthogonal construction: Two cylinders intersect perpendicularly
- Equal radius: Both cylinders have identical radius r
- Central intersection: The cylinder axes intersect at the center
- 6 identical surfaces: Each surface is a curved surface
- 12 edges: All edges have length 2r
- High symmetry: 9 mirror planes and 3-fold rotational symmetry
- Mathematical elegance: All formulas contain the factor 16
Versatile Applications
Architectural Beauty
In architecture, the bicylinder is used for column connections, dome constructions, and sculptural elements.
Technical Precision
In mechanical engineering, it finds application in pipe connections, joint parts, and complex machine elements.
Scientific Significance
In crystallography and materials science, it serves as a model for complex structures and symmetry analyses.
Artistic Inspiration
As a sculptural element, the bicylinder embodies the perfect balance between geometric rigor and aesthetic appeal.
Summary
The bicylinder embodies the perfect harmony between mathematical elegance and practical application. Its form, created by orthogonal cylinder intersection and described by elegant formulas with the characteristic factor 16, makes it a fundamental building block of geometry. From architectural masterpieces to technical precision parts to artistic sculptures - the bicylinder connects theoretical beauty with practical utility. As a Steinmetz solid, it shows how the simple intersection of two cylinders leads to one of the most symmetric and elegant geometric bodies in mathematics, enriching our world from the smallest technical application to the grandest architectural vision.