Half Cylinder Calculator
Calculator and formulas for calculating a half cylinder
Half Cylinder Calculator
The Half Cylinder
The half cylinder is a halved circular cylinder with a semicircular base.
Half Cylinder Properties
The Half Cylinder: Half of a circular cylinder with semicircular base
Half Cylinder Visualization
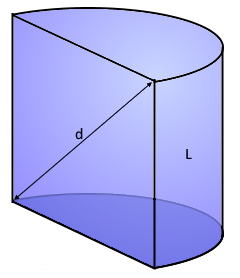
Half Cylinder
Half of a circular cylinder
Components
Semicircular bases: 2 × (πr²/2)
Curved lateral surface: πrh
Rectangular cut surface: 2rh
Halved circular cylinder.
Exactly half the volume.
|
|
What is a Half Cylinder?
The half cylinder is an important geometric body:
- Definition: Exact half of a circular cylinder through axial division
- Base: Two semicircular end surfaces
- Properties: Curved lateral surface plus flat cut surface
- Symmetry: One plane of symmetry through the cut surface
- Applications: Architecture, piping, roofing
- Mathematics: Simple relationship to full cylinder (factor 1/2)
Geometric Properties of the Half Cylinder
The half cylinder shows characteristic geometric properties:
Basic Parameters
- Radius r: Radius of the original circular base
- Height h: Distance between the semicircular end surfaces
- Diameter: Diameter of the cut surface = 2r
- Diagonal: √(h² + (2r)²) through the entire body
Special Properties
- Five surfaces: 2 semicircles + 1 curved + 1 rectangular surface
- Edges: 2 straight edges on the cut surface
- Symmetry: One plane of symmetry through the longitudinal axis
- Halving: Exactly half of all cylinder parameters
Mathematical Relationships of the Half Cylinder
The half cylinder follows elegant mathematical laws:
Volume Formula
The volume is exactly half of a full cylinder. Simple and logical.
Surface Area Formula
Combination of curved lateral surface and additional rectangular cut surface.
Applications of the Half Cylinder
Half cylinders find applications in various fields:
Architecture & Construction
- Barrel roofs and vaults
- Semicircular windows and doors
- Bridge elements
- Tunnel and subway constructions
Technology & Industry
- Halved pipelines
- Gutters and channels
- Bulk material containers
- Machine components
Water Engineering & Hydraulics
- Semicircular channels
- Rain gutters
- Sewage pipes
- Irrigation systems
Design & Art
- Sculptural elements
- Furniture design
- Decoration and ornaments
- Landscape architecture
Formulas for the Half Cylinder
Volume (V)
Half the volume of the corresponding full cylinder
Lateral Area (L)
Curved lateral surface (half cylinder circumference)
Total Surface Area (S)
Lateral area + semicircles + rectangular surface
Diagonal (d)
Diagonal through the entire half cylinder
Surface Area Breakdown
\[A_{Semicircles} = \pi r^2\]
\[A_{Lateral} = \pi r h\]
\[A_{Rectangle} = 2rh\]
\[S = \sum A_i\]
The half cylinder consists of five different surface parts
Calculation Example for a Half Cylinder
Given
Find: All parameters of the half cylinder
1. Volume Calculation
For r = 5 cm, h = 12 cm:
\[V = \frac{1}{2} \cdot \pi \cdot r^2 \cdot h\] \[V = \frac{1}{2} \cdot \pi \cdot 5^2 \cdot 12\] \[V = \frac{1}{2} \cdot \pi \cdot 25 \cdot 12\] \[V = 150\pi ≈ 471.24 \text{ cm}^3\]The volume is approximately 471.24 cm³
2. Lateral Area Calculation
Curved lateral surface:
\[L = \pi \cdot r \cdot h\] \[L = \pi \cdot 5 \cdot 12\] \[L = 60\pi ≈ 188.50 \text{ cm}^2\]The lateral area is approximately 188.50 cm²
3. Surface Area Calculation
Individual surface components:
\[A_{Semicircles} = \pi r^2 = 25\pi ≈ 78.54 \text{ cm}^2\] \[A_{Rectangle} = 2rh = 2 \cdot 5 \cdot 12 = 120 \text{ cm}^2\] \[S = 188.50 + 78.54 + 120 ≈ 387.04 \text{ cm}^2\]The total surface area is approximately 387.04 cm²
4. Diagonal Calculation
Diagonal through the half cylinder:
\[d = \sqrt{h^2 + (2r)^2}\] \[d = \sqrt{12^2 + 10^2}\] \[d = \sqrt{144 + 100} = \sqrt{244}\] \[d ≈ 15.62 \text{ cm}\]The diagonal is approximately 15.62 cm
5. Summary
The half cylinder with all characteristic parameters
6. Comparison with Full Cylinder
r=5, h=12
V≈471.24 cm³
r=5, h=12
V≈942.48 cm³
1 : 2
Exactly half
The half cylinder has exactly half the volume of the corresponding full cylinder
7. Practical Example: Rain Gutter
V ≈ 471.24 cm³
≈ 0.47 liters
S ≈ 387.04 cm²
Sheet metal area
Per meter: 39.3 L
At h=1m
A practical rain gutter with r=5cm holds about 39 liters per meter length
The Half Cylinder: Elegance of Half Symmetry
The half cylinder is a fascinating geometric body that combines the elegance of cylinder symmetry with the functionality of an open structure. As an exact half of a circular cylinder, it retains the characteristic properties of the curved lateral surface, but extends them with the practical accessibility of a flat cut surface. This combination makes it one of the most versatile and practical geometric bodies in architecture, technology, and design.
The Geometry of Halving
The half cylinder shows the perfection of axial division:
- Exact halving: Perfect division along the cylinder axis
- Semicircular base: Two semicircular end surfaces
- Curved lateral surface: Half cylinder circumference over height
- Rectangular cut surface: Flat surface with dimensions 2r × h
- Plane of symmetry: One mirror plane through the longitudinal axis
- Simple formulas: All parameters with factor 1/2 from full cylinder
- Practical opening: Accessibility through the cut surface
Versatile Applications
Architectural Functionality
Barrel roofs and vault constructions use structural stability with optimal space utilization and weather protection.
Hydraulic Efficiency
Semicircular channels and gutters maximize water flow with minimal material consumption and optimal self-cleaning.
Technical Superiority
In industry, half-cylindrical structures enable optimal material distribution and simple manufacturing with high load capacity.
Aesthetic Elegance
The harmonious connection of curved and flat surfaces creates aesthetically pleasing and functionally optimized forms.
Summary
The half cylinder embodies the perfect balance between geometric elegance and practical functionality. Its form, created by axial halving, with the characteristic combination of curved lateral surface and flat cut surface, makes it one of the most versatile geometric bodies. The simple mathematical relationships (factor 1/2 to full cylinder) combined with practical accessibility show how elegant geometry and technical utility harmonize. From monumental barrel roofs to efficient water channels to aesthetic design elements - the half cylinder proves that halving a geometric body often leads to double functionality and shows how reduction to the essential can become maximum versatility.