Regular Pyramid Calculator
Calculator and formulas for regular pyramids with any number of sides (n-gonal pyramids)
N-Gonal Pyramid Calculator
The Regular Pyramid
A regular pyramid has a regular n-sided polygon as its base and n identical triangular faces meeting at the apex.
Regular Pyramid Properties
Universal formula: Works for any regular n-sided polygon base
Regular Pyramid Structure
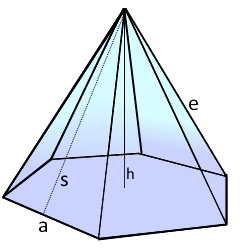
Regular n-sided pyramid with perfect symmetry.
Universal formulas for any polygon base.
|
|
What is a regular pyramid?
A regular pyramid is a fundamental geometric shape with universal applicability:
- Definition: A pyramid with a regular polygon as its base
- Base: Any regular n-sided polygon (triangle, square, pentagon, etc.)
- Faces: 1 regular n-gon base + n identical triangular faces
- Vertices: n+1 vertices (n on base, 1 apex)
- Edges: 2n edges (n base edges, n lateral edges)
- Symmetry: n-fold rotational symmetry
Geometric Properties of Regular Pyramids
Regular pyramids exhibit remarkable universal geometric properties:
Universal Parameters
- Faces: n+1 faces total (1 base + n triangles)
- Vertices: n+1 vertices (n on base, 1 apex)
- Edges: 2n edges (n base, n lateral)
- Euler characteristic: V - E + F = (n+1) - 2n + (n+1) = 2
Special Properties
- Regular base: All base sides and angles are equal
- Identical faces: All triangular faces are congruent
- Perfect symmetry: n-fold rotational symmetry
- Convex: All vertices point outward
Mathematical Relationships
Regular pyramids follow elegant universal mathematical laws:
Volume Formula
Universal pyramid volume formula. Works for any regular base.
Base Area Formula
Involves cotangent function. Universal for any n-gon.
Applications of Regular Pyramids
Regular pyramids find applications across numerous fields:
Architecture & Construction
- Pyramid structures and monuments
- Roof designs and spires
- Decorative architectural elements
- Landscaping and garden features
Science & Technology
- Crystal structures and mineralogy
- Molecular geometry and chemistry
- Antenna design and radar systems
- Optical systems and prisms
Education & Research
- Geometry education and demonstrations
- 3D modeling and visualization
- Mathematical research and analysis
- Engineering design principles
Engineering & Manufacturing
- Mechanical component design
- Structural supports and brackets
- Container and hopper design
- Precision tooling and fixtures
Regular Pyramid Formulas
Base Area (A)
Universal formula for regular n-gon area
Volume (V)
Universal pyramid volume formula
Slant Height (s)
From center of base to apex via face center
Edge Length (e)
Length of lateral edges from base vertices to apex
Lateral Surface (AL)
Total area of all triangular faces
Surface Area (S)
Base area plus lateral surface area
Additional Formulas
\(A_s = \frac{a \cdot s}{2}\)
\(P = n \cdot a\)
\(r = \frac{a}{2 \tan\left(\frac{\pi}{n}\right)}\)
Supporting calculations for regular pyramid analysis
Calculation Example for a Regular Pyramid
Given - Pentagonal Pyramid
Find: All properties of the regular pentagonal pyramid
1. Base Area Calculation
Pentagon base area:
\[A = \frac{5 \cdot 6^2}{4 \cdot \tan\left(\frac{\pi}{5}\right)}\] \[A = \frac{5 \cdot 36}{4 \cdot \tan(36°)}\] \[A = \frac{180}{4 \cdot 0.7265} ≈ 61.94\]The pentagon base area is approximately 61.94 square units
2. Volume Calculation
Pyramid volume:
\[V = \frac{A \cdot h}{3} = \frac{61.94 \cdot 8}{3}\] \[V = \frac{495.52}{3} ≈ 165.17\]The volume is approximately 165.17 cubic units
3. Slant Height Calculation
Slant height to face center:
\[s = \sqrt{8^2 + \frac{6^2 \cdot \cot^2\left(\frac{\pi}{5}\right)}{4}}\] \[s = \sqrt{64 + \frac{36 \cdot 1.376^2}{4}}\] \[s = \sqrt{64 + 17.04} ≈ 9.00\]The slant height is approximately 9.00 units
4. Surface Area Calculation
Lateral surface area:
\[A_L = \frac{5 \cdot 6 \cdot 9.00}{2} = \frac{270}{2} = 135\]Total surface area:
\[S = 61.94 + 135 = 196.94\]Total surface area is approximately 196.94 square units
Complete Pentagonal Pyramid Results
Perfect regular pentagonal pyramid with universal mathematical relationships
The Regular Pyramid: Universal Mathematical Perfection
The regular pyramid represents one of the most fundamental and versatile geometric forms in mathematics and engineering. This remarkable shape, characterized by its regular polygonal base and identical triangular faces meeting at a single apex, embodies the perfect marriage of symmetry and functionality. The mathematical beauty of regular pyramids lies in their universal formulas that work seamlessly for any number of base sides, from the simplest triangular pyramid (tetrahedron) to complex polygonal pyramids with dozens of sides, each maintaining perfect geometric relationships through elegant trigonometric expressions.
The Geometry of Universal Symmetry
Regular pyramids showcase the ultimate in geometric versatility and symmetry:
- Universal applicability: Single formula set works for any n-sided base
- Perfect symmetry: n-fold rotational symmetry around the central axis
- Identical faces: All lateral faces are congruent isosceles triangles
- Regular base: All base sides and angles are perfectly equal
- Trigonometric elegance: Formulas involve fundamental trig functions
- Scalable precision: Maintains proportions at any size
- Structural efficiency: Optimal material distribution for strength
Mathematical Elegance and Universality
Trigonometric Foundation
The base area formula using tangent and cotangent functions provides universal applicability, automatically adjusting for any number of sides while maintaining mathematical precision.
Pythagorean Relationships
The slant height and edge length calculations elegantly combine the Pythagorean theorem with trigonometric principles, creating robust geometric relationships.
Universal Volume Principle
The fundamental pyramid volume formula (base area × height ÷ 3) works universally, regardless of base complexity, demonstrating mathematical consistency.
Geometric Scaling
All formulas scale perfectly, maintaining proportional relationships across different sizes while preserving the inherent geometric beauty of the regular pyramid.
Summary
The regular pyramid stands as a testament to the power of universal mathematical principles in geometry. Its elegant formulas, incorporating trigonometric functions and geometric relationships, provide a single mathematical framework that seamlessly handles pyramids with any number of base sides. From the fundamental tetrahedron to complex polygonal pyramids, these universal relationships maintain perfect consistency while adapting to any geometric complexity. This mathematical universality makes regular pyramids invaluable in engineering, architecture, and scientific applications where precise calculations and predictable behavior are essential. The beauty of these formulas lies not just in their mathematical elegance, but in their practical utility, providing engineers and designers with reliable tools for creating structures that are both geometrically perfect and structurally sound. Understanding regular pyramid mathematics opens the door to comprehending the fundamental principles that govern three-dimensional geometric relationships across countless applications.