Absolute Value
Definition, properties, and applications for real and complex numbers
Introduction to Absolute Value
The absolute value of a number is a fundamental concept in mathematics that measures the distance of a number from zero, without regard to direction. It is always a non-negative number.
The absolute value is also known as the modulus or magnitude of a number. This concept applies to both real numbers and complex numbers, and has important applications in algebra, calculus, and many other areas of mathematics.
The absolute value represents the distance from a number to zero on the number line (for real numbers) or the distance from the origin in the complex plane (for complex numbers). Since distance is always non-negative, the absolute value is always greater than or equal to zero.
Absolute Value of Real Numbers
For real numbers, the absolute value is obtained by removing the sign. Geometrically, it represents the distance from a number to zero on the number line.
The absolute value of a real number \(x\), denoted \(\displaystyle |x|\), is defined as:
\(\displaystyle |x| = \begin{cases} x & \text{if } x \geq 0 \\ -x & \text{if } x < 0 \end{cases}\)
In simpler terms: remove the negative sign if present.
Examples of Absolute Value for Real Numbers
- \(\displaystyle |5| = 5\) (5 is already positive)
- \(\displaystyle |-5| = 5\) (remove the negative sign)
- \(\displaystyle |0| = 0\) (zero is its own absolute value)
- \(\displaystyle |-3.7| = 3.7\) (works with decimals)
- \(\displaystyle \left|-\frac{1}{2}\right| = \frac{1}{2}\) (works with fractions)
Absolute Value of Complex Numbers
For complex numbers, the absolute value (also called the modulus) represents the distance from the complex number to the origin in the complex plane.
For a complex number \(\displaystyle z = a + bi\) where \(a, b \in \mathbb{R}\), the absolute value (modulus) is:
\(\displaystyle |z| = |a + bi| = \sqrt{a^2 + b^2}\)
This formula comes from the Pythagorean theorem, treating the real and imaginary parts as the legs of a right triangle.
Examples of Absolute Value for Complex Numbers
- \(\displaystyle |3 + 4i| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\)
- \(\displaystyle |1 + i| = \sqrt{1^2 + 1^2} = \sqrt{2} \approx 1.414\)
- \(\displaystyle |5 + 0i| = \sqrt{5^2 + 0^2} = 5\) (real numbers are complex with \(b = 0\))
- \(\displaystyle |0 + 3i| = \sqrt{0^2 + 3^2} = 3\) (purely imaginary)
- \(\displaystyle |-2 - 2i| = \sqrt{(-2)^2 + (-2)^2}\)\(\displaystyle = \sqrt{8} = 2\sqrt{2} \approx 2.828\)
Geometric Interpretation in the Complex Plane
In the complex plane (Argand diagram), a complex number \(\displaystyle z = a + bi\) is represented as a point \((a, b)\). The absolute value is the distance from this point to the origin.
Complex Plane Interpretation:
The complex number \(\displaystyle 3 + 4i\) is at point (3, 4)
Its distance from the origin is \(\displaystyle |3 + 4i| = 5\)
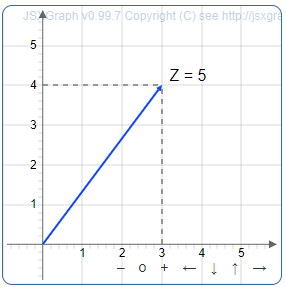
Any real number \(x\) can be written as a complex number \(\displaystyle x + 0i\). Its absolute value is \(\displaystyle |x + 0i| = \sqrt{x^2 + 0^2} = |x|\), which matches the definition for real numbers.
Properties of Absolute Value
The absolute value has several important mathematical properties that are useful in algebra and calculus.
Non-negativity
\(\displaystyle |x| \geq 0\)The absolute value is always non-negative. It equals zero only when \(\displaystyle x = 0\).
Triangle Inequality
\(\displaystyle |x + y| \leq |x| + |y|\)The absolute value of a sum is less than or equal to the sum of absolute values.
Product Rule
\(\displaystyle |xy| = |x| \cdot |y|\)The absolute value of a product equals the product of absolute values.
Quotient Rule
\(\displaystyle \left|\frac{x}{y}\right| = \frac{|x|}{|y|}\) (where \(y \neq 0\))The absolute value of a quotient equals the quotient of absolute values.
Symmetry
\(\displaystyle |x| = |-x|\)A number and its opposite have the same absolute value.
Power Rule
\(\displaystyle |x^n| = |x|^n\)For any positive integer \(n\), this property holds.
Examples of Properties
Demonstrating Properties
Non-negativity:
- \(\displaystyle |-7| = 7 \geq 0\) ✓
- \(\displaystyle |0| = 0 \geq 0\) ✓
Product Rule:
- \(\displaystyle |-3 \cdot 4| = |-12| = 12 = |-3| \cdot |4| = 3 \cdot 4\) ✓
Triangle Inequality:
- \(\displaystyle |-2 + 5| = |3| = 3 \leq |-2| + |5| = 2 + 5 = 7\) ✓
Symmetry:
- \(\displaystyle |8| = 8 = |-8|\) ✓
Applications of Absolute Value
Solving Absolute Value Equations
Equations containing absolute values require special attention because each absolute value creates multiple cases.
Example: Solve \(\displaystyle |x - 3| = 5\)
This equation has two cases:
Case 1: \(\displaystyle x - 3 = 5 \Rightarrow x = 8\)
Case 2: \(\displaystyle x - 3 = -5 \Rightarrow x = -2\)
Solutions: \(\displaystyle x = 8\) or \(\displaystyle x = -2\)
Distance and Measurement
- Distance between two points: \(\displaystyle |a - b|\) gives the distance between \(a\) and \(b\)
- Error magnitude: In measurements and approximations
- Modulus in signal processing: Determining signal strength
- Tolerance ranges: In engineering and manufacturing
Mathematical Analysis
- Limits and continuity: Defining epsilon-delta proofs
- Inequalities: Solving absolute value inequalities
- Norms in linear algebra: Measuring vector magnitudes
- Series convergence: Testing convergence conditions
Absolute Value Inequalities
Inequalities with absolute values are common in mathematics. Here are the key patterns:
| Inequality | Equivalent Form | Solution Example |
|---|---|---|
| \(\displaystyle |x| < a\) (where \(a > 0\)) | \(\displaystyle -a < x < a\) | \(\displaystyle |x| < 3 \Rightarrow -3 < x < 3\) |
| \(\displaystyle |x| > a\) (where \(a > 0\)) | \(\displaystyle x < -a\) or \(\displaystyle x > a\) | \(\displaystyle |x| > 2 \Rightarrow x < -2\) or \(\displaystyle x > 2\) |
| \(\displaystyle |x| \leq a\) (where \(a > 0\)) | \(\displaystyle -a \leq x \leq a\) | \(\displaystyle |x| \leq 4 \Rightarrow -4 \leq x \leq 4\) |
| \(\displaystyle |x| \geq a\) (where \(a > 0\)) | \(\displaystyle x \leq -a\) or \(\displaystyle x \geq a\) | \(\displaystyle |x| \geq 1 \Rightarrow x \leq -1\) or \(\displaystyle x \geq 1\) |
Summary: Absolute Value Definitions
| Type of Number | Notation | Definition | Example |
|---|---|---|---|
| Real (Positive) | \(\displaystyle |x|\) | \(\displaystyle |x| = x\) | \(\displaystyle |7| = 7\) |
| Real (Negative) | \(\displaystyle |x|\) | \(\displaystyle |x| = -x\) | \(\displaystyle |-7| = 7\) |
| Zero | \(\displaystyle |0|\) | \(\displaystyle |0| = 0\) | \(\displaystyle |0| = 0\) |
| Complex | \(\displaystyle |z|\) | \(\displaystyle |a+bi| \)\(\displaystyle = \sqrt{a^2+b^2}\) | \(\displaystyle |3+4i| = 5\) |
Common Mistakes to Avoid
WRONG: \(\displaystyle |a + b| = |a| + |b|\) (always) ✗
RIGHT: \(\displaystyle |a + b| \leq |a| + |b|\) (Triangle Inequality) ✓
WRONG: \(\displaystyle |x - 2| = 3\) has only one solution ✗
RIGHT: \(\displaystyle |x - 2| = 3\) gives \(\displaystyle x = 5\) or \(\displaystyle x = -1\) ✓
WRONG: \(\displaystyle |x| < 5 \Rightarrow x < 5\) (incomplete) ✗
RIGHT: \(\displaystyle |x| < 5 \Rightarrow -5 < x < 5\) ✓
|
|