Absoluter Betrag einer Zahl
Beschreibung des absoluten Betrags einer reellen oder komplexen Zahl
Der Absolutwert einer reellen oder komplexen Zahl ist ihr Abstand zu Null. Dieser sogenannte absolute Betrag, Absolutbetrag, Absolutwert oder auch schlicht Betrag ist immer eine positive reelle Zahl.
Absolutwert einer reellen Zahl
Einfach ausgedrückt erhält man den absoluten Betrag einer reellen Zahl durch Weglassen des Vorzeichens. Wenn reelle Zahlen auf einer Zahlengeraden dargestellt werden, liegen die negativen Zahlen links vom Nullpunkt und die positiven Zahlen rechts vom Nullpunkt.
Den Absolutbetrag oder Betrag einer reellen Zahl ist der Abstand vom Nullpunkt auf der Zahlengeraden. Der Absolutbetrag einer reellen Zahl \(x\) wird als \(|x|\), oder als Funktion \(abs(x)\) geschrieben.
Der Absolutbetrag von 3 ist gleich 3 \(|3| = 3\)
Der Absolutbetrag von -3 ist auch 3 |-\(3| = 3\)
Der Absolutbetrag von 0 ist gleich 0 \(|0|=0\)
Betrag einer komplexen Zahl
Die Darstellung mittels Ortsvektoren einer komplexen Zahl ergibt immer ein rechtwinkliges Dreieck, das aus den beiden Katheten \(a\) und \(b\) und der Hypotenuse \(z\) besteht. Der Betrag oder Wert einer komplexen Zahl entspricht der Länge des Ortsvektors.
Der Betrag einer komplexen Zahl \(z = a + bi\) ist also \(|z|=\sqrt{a^2+b^2}\)
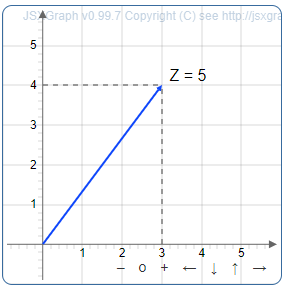
Die Abbildung unten zeigt die grafische Darstellung der komplexen Zahl \(3 + 4i\) und deren Betrag \(|z| = 5\).
|
|