Complex Numbers
Complete guide to complex number theory, operations, and graphical representation
Introduction to Complex Numbers
Complex numbers extend the real number system to solve problems that have no real solutions. They form the foundation of advanced mathematics, engineering, and physics, enabling us to work with equations that would otherwise have no solution.
Consider the quadratic equation \(\displaystyle x^2 + 1 = 0\) or \(\displaystyle x^2 = -1\). No real number squared equals -1, since the square of any real number is non-negative. To solve such equations, we need to introduce complex numbers.
Definition of Complex Numbers
In order to solve equations like \(\displaystyle x^2 = -1\), the mathematician Leonhard Euler introduced the imaginary unit \(i\), defined by the property:
\(\displaystyle i^2 = -1\) or \(\displaystyle i = \sqrt{-1}\)
A complex number \(z\) consists of two parts: a real part and an imaginary part.
A complex number is a number of the form:
\(\displaystyle z = a + bi\)
where \(a, b \in \mathbb{R}\) and \(i = \sqrt{-1}\)
Real Part
\(\displaystyle \text{Re}(z) = a\)Imaginary Part
\(\displaystyle \text{Im}(z) = b\)Modulus (Absolute Value)
\(\displaystyle |z| = \sqrt{a^2 + b^2}\)Examples of Complex Numbers
- \(\displaystyle z_1 = 3 + 4i\) (real part = 3, imaginary part = 4)
- \(\displaystyle z_2 = -2 + i\) (real part = -2, imaginary part = 1)
- \(\displaystyle z_3 = 5\) (real part = 5, imaginary part = 0, purely real)
- \(\displaystyle z_4 = 2i\) (real part = 0, imaginary part = 2, purely imaginary)
- \(\displaystyle z_5 = -3 - 5i\) (real part = -3, imaginary part = -5)
If \(\displaystyle b = 0\), then \(\displaystyle z = a\) is a real number. If \(\displaystyle a = 0\), then \(\displaystyle z = bi\) is a purely imaginary number. The set of all complex numbers is denoted by \(\mathbb{C}\).
Graphical Representation: The Argand Plane
Complex numbers can be represented graphically using the Argand plane (also called the complex plane). This is a coordinate system where:
- Horizontal axis (Real axis): represents the real part \(a\)
- Vertical axis (Imaginary axis): represents the imaginary part \(b\)
Each complex number \(\displaystyle z = a + bi\) corresponds to a point \((a, b)\) in the Argand plane.
Example: Complex Number z = 3 + 4i
In the Argand plane, the point is located at coordinates (3, 4).
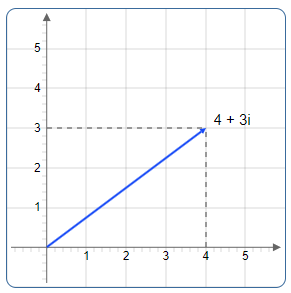
The modulus (absolute value) is the distance from the origin to the point:
The modulus \(\displaystyle |z| = \sqrt{a^2 + b^2}\) represents the distance from the origin to the point representing the complex number in the Argand plane. It corresponds to the length of the vector from the origin to \((a, b)\).
Operations with Complex Numbers
Addition and Subtraction
Complex numbers are added and subtracted by combining their real and imaginary parts separately:
\(\displaystyle (a + bi) + (c + di) = (a + c) + (b + d)i\)
\(\displaystyle (a + bi) - (c + di) = (a - c) + (b - d)i\)
Examples
Addition:
Subtraction:
Multiplication
Multiplication is performed by expanding the product and remembering that \(\displaystyle i^2 = -1\):
\(\displaystyle (a + bi)(c + di) = ac + adi + bci + bdi^2\)
\(\displaystyle = ac + adi + bci - bd = (ac - bd) + (ad + bc)i\)
Example of Multiplication
\(\displaystyle = 2 + 4i + 3i + 6i^2 = 2 + 7i - 6 = -4 + 7i\)
Complex Conjugate and Division
The complex conjugate of \(\displaystyle z = a + bi\) is denoted \(\displaystyle \overline{z} = a - bi\).
If \(\displaystyle z = a + bi\), then \(\displaystyle \overline{z} = a - bi\)
Note: \(\displaystyle z \cdot \overline{z} = (a + bi)(a - bi) = a^2 + b^2\)
Division is performed by multiplying numerator and denominator by the conjugate of the denominator:
\(\displaystyle \frac{a + bi}{c + di} = \frac{(a + bi)(c - di)}{(c + di)(c - di)} = \frac{(a + bi)(c - di)}{c^2 + d^2}\)
Example of Division
\(\displaystyle = \frac{3 - i + 2}{1 + 1} = \frac{5 - i}{2} = \frac{5}{2} - \frac{1}{2}i\)
Important Properties of Complex Numbers
| Formula | Example |
|---|---|
| Modulus | |
| \(\displaystyle |a + bi| = \sqrt{a^2 + b^2}\) | \(\displaystyle |3 + 4i| = 5\) |
| Conjugate | |
| \(\displaystyle \overline{a + bi} = a - bi\) | \(\displaystyle \overline{2 + 3i} = 2 - 3i\) |
| Product with Conjugate | |
| \(\displaystyle z \cdot \overline{z} = a^2 + b^2\) | \(\displaystyle (2 + 3i)(2 - 3i) = 13\) |
| Modulus of Product | |
| \(\displaystyle |z_1 \cdot z_2| = |z_1| \cdot |z_2|\) | \(\displaystyle |2 + 3i| \cdot |1 + i| = |..|\) |
| Modulus of Quotient | |
| \(\displaystyle \left|\frac{z_1}{z_2}\right| = \frac{|z_1|}{|z_2|}\) | \(\displaystyle \frac{|3 + 4i|}{|1 + i|} = \frac{5}{\sqrt{2}}\) |
Powers of the Imaginary Unit
The powers of \(i\) follow a cyclic pattern with period 4:
| Power | Value | Description |
|---|---|---|
| \(\displaystyle i^1\) | \(\displaystyle i\) | Imaginary unit |
| \(\displaystyle i^2\) | \(\displaystyle -1\) | Definition of imaginary unit |
| \(\displaystyle i^3\) | \(\displaystyle -i\) | \(i^2 \cdot i = -1 \cdot i\) |
| \(\displaystyle i^4\) | \(\displaystyle 1\) | \(i^2 \cdot i^2 = (-1)(-1)\) |
| \(\displaystyle i^5\) | \(\displaystyle i\) | Pattern repeats: \(i^5 = i^4 \cdot i = i\) |
Since the powers repeat with period 4, to find \(\displaystyle i^n\) for any \(n\), divide \(n\) by 4 and use the remainder: \(\displaystyle i^n = i^{n \bmod 4}\).
Complex Numbers in the Number Hierarchy
\(\displaystyle \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C}\)
Naturals ⊂ Integers ⊂ Rationals ⊂ Reals ⊂ Complex
| Number Set | Symbol | Description |
|---|---|---|
| Natural | ℕ | 0, 1, 2, 3, ... (counting numbers) |
| Integer | ℤ | ..., -2, -1, 0, 1, 2, ... |
| Rational | ℚ | a/b where a, b ∈ ℤ, b ≠ 0 |
| Real | ℝ | All rational and irrational numbers |
| Complex | ℂ | a + bi where a, b ∈ ℝ |
Applications of Complex Numbers
- Engineering: Analysis of AC circuits and signal processing
- Physics: Quantum mechanics and wave functions
- Mathematics: Solving polynomial equations and calculus
- Computer Science: Fourier transforms and image processing
- Navigation: Representing rotations and transformations in 2D
- Control Theory: Analyzing system stability and response
|
|