Komplexe Zahlen
Grundlagen zur Definition und Anwendung komplexer Zahlen
Dieser Artikel gibt eine umfassende Einführung in die Grundlagen zum Rechnen mit komplexen Zahlen. Komplexe Zahlen erweitern die reellen Zahlen und ermöglichen es, Lösungen für Gleichungen zu finden, die im reellen Zahlensystem keine Lösung haben. Detailliertere Beschreibungen finden Sie in dem Kapitel über Komplexe Zahlen.
Definition einer komplexen Zahl
Das Problem mit quadratischen Gleichungen
Mit quadratischen Gleichungen gibt es nicht immer eine Lösung im reellen Zahlensystem. Beispielsweise die Gleichung:
Im reellen Zahlensystem gibt es keine Zahl, deren Quadrat -1 ergibt. Um trotzdem mit Lösungen von solchen Gleichungen rechnen zu können, verwenden wir eine neue, imaginäre Zahl, die mit dem Buchstaben i bezeichnet wird.
Die imaginäre Einheit i ist definiert als die Lösung der Gleichung x² = -1. Es gilt: i² = -1
Struktur einer komplexen Zahl
Eine komplexe Zahl z besteht aus zwei Komponenten:
- Realteil (a): Eine reelle Zahl
- Imaginärteil (b): Eine reelle Zahl, multipliziert mit i
z = a + bi
wobei a, b ∈ ℝ (reelle Zahlen) und i die imaginäre Einheit ist
Beispiele komplexer Zahlen
- z₁ = 3 + 4i (Realteil: 3, Imaginärteil: 4)
- z₂ = -2 + i (Realteil: -2, Imaginärteil: 1)
- z₃ = 5 - 3i (Realteil: 5, Imaginärteil: -3)
- z₄ = 2i (Realteil: 0, Imaginärteil: 2) - Rein imaginär
- z₅ = 7 (Realteil: 7, Imaginärteil: 0) - Rein reell
Reelle Zahlen sind ein Spezialfall komplexer Zahlen, bei denen der Imaginärteil b = 0 ist. Somit gelten reelle Zahlen auch als komplexe Zahlen: ℝ ⊂ ℂ
Betrag einer komplexen Zahl
Der Betrag (auch Modul oder Absolutwert genannt) einer komplexen Zahl entspricht der Länge des Vektors in der Gauß'schen Ebene.
|z| = |a + bi| = √(a² + b²)
Beispiele für Beträge
- z = 3 + 4i: |z| = √(3² + 4²) = √(9 + 16) = √25 = 5
- z = -2 + i: |z| = √((-2)² + 1²) = √(4 + 1) = √5 ≈ 2,236
- z = 5 - 3i: |z| = √(5² + (-3)²) = √(25 + 9) = √34 ≈ 5,831
Grafische Darstellung komplexer Zahlen
Die Gauß'sche Zahlenebene
Um komplexe Zahlen grafisch zu interpretieren, wird die Gauß'sche Zahlenebene (auch komplexe Ebene oder Argand-Diagramm genannt) verwendet. Dies ist eine spezielle Form eines kartesischen Koordinatensystems.
- Horizontale Achse (X-Achse): Reelle Achse - zeigt den Realteil a
- Vertikale Achse (Y-Achse): Imaginäre Achse - zeigt den Imaginärteil b
Jede komplexe Zahl z = a + bi wird als Punkt P(a, b) in dieser Ebene dargestellt. Der Abstand vom Ursprung zum Punkt entspricht dem Betrag |z| der komplexen Zahl.
Darstellung: z = 3 + 4i
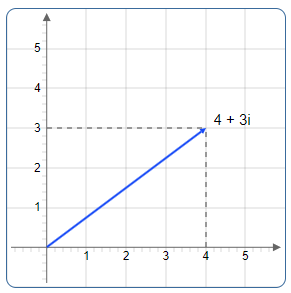
Erklärung: Die komplexe Zahl 3 + 4i wird im Punkt (3, 4) dargestellt. Der Betrag ist |z| = 5, was der Länge des Vektors vom Ursprung zu diesem Punkt entspricht.
Punkt
z = a + bi wird als Punkt P(a, b) dargestellt
Vektor
z kann als Vektor vom Ursprung zum Punkt (a, b) angesehen werden
Betrag
Der Betrag |z| ist die Länge des Vektors: √(a² + b²)
Argument
Das Argument ist der Winkel φ zwischen Vektor und reeller Achse
Polarform (Exponentialform)
Neben der Normalform a + bi gibt es auch die Polarform, die eine alternative Darstellung komplexer Zahlen ist.
Darstellungsformen:
Normalform: z = a + bi
Polarform (trigonometrisch): z = r(cos φ + i sin φ)
Exponentialform (Euler): z = r·e^(iφ)
wobei r = |z| der Betrag und φ das Argument ist
Beispiel: Umrechnung in Polarform
Gegeben: z = 3 + 4i
- Betrag: r = √(3² + 4²) = 5
- Argument: φ = arctan(4/3) ≈ 0,927 rad ≈ 53,13°
- Polarform: z = 5(cos 53,13° + i sin 53,13°)
- Exponentialform: z = 5e^(i·0,927)
Operationen mit komplexen Zahlen
Addition komplexer Zahlen
Bei der Addition werden Real- und Imaginärteile getrennt addiert:
Beispiel
- (3 + 4i) + (2 + i) = (3 + 2) + (4 + 1)i = 5 + 5i
Subtraktion komplexer Zahlen
Bei der Subtraktion werden Real- und Imaginärteile getrennt subtrahiert:
Beispiel
- (5 + 3i) - (2 + i) = (5 - 2) + (3 - 1)i = 3 + 2i
Multiplikation komplexer Zahlen
Die Multiplikation erfolgt wie die Multiplikation von Binomen, mit Beachtung von i² = -1:
Beispiel
- (2 + 3i) · (1 + 2i) = 2·1 + 2·2i + 3i·1 + 3i·2i
- = 2 + 4i + 3i + 6i² = 2 + 7i - 6 = -4 + 7i
Division komplexer Zahlen
Bei der Division wird mit dem konjugiert komplexen Nenner erweitert. Die konjugiert komplexe Zahl zu a + bi ist a - bi.
Beispiel
- (3 + 4i) / (1 + 2i)
- = [(3 + 4i)·(1 - 2i)] / [(1 + 2i)·(1 - 2i)]
- = [3 - 6i + 4i - 8i²] / [1 - 4i²] = [3 - 2i + 8] / 5 = (11 - 2i) / 5 = 2,2 - 0,4i
Konjugiert komplexe Zahlen
Für jede komplexe Zahl z = a + bi gibt es die konjugiert komplexe Zahl z̄ = a - bi.
Die konjugiert komplexe Zahl zu z = a + bi ist z̄ = a - bi. Geometrisch ist dies eine Spiegelung an der reellen Achse.
Beispiele
- z = 3 + 4i → z̄ = 3 - 4i
- z = -2 + i → z̄ = -2 - i
- z = 5 - 3i → z̄ = 5 + 3i
Eigenschaften konjugiert komplexer Zahlen
- z · z̄ = |z|² (Produkt mit Konjugat = Betrag zum Quadrat)
- z + z̄ = 2·Re(z) (Summe = doppelter Realteil)
- z - z̄ = 2i·Im(z) (Differenz = doppelter Imaginärteil mal i)
- z̄̄ = z (Konjugation der Konjugation ergibt die ursprüngliche Zahl)
Praktische Anwendungen
- Elektrotechnik: Impedanz und Wechselstromberechnung
- Signalverarbeitung: Fourier-Analyse und Filter
- Quantenmechanik: Wellenfunktionen und Wahrscheinlichkeitsamplituden
- Fluiddynamik: Potential-Strömungen mit komplexem Potential
- Kontrolltheorie: Pole und Nullstellen von Übertragungsfunktionen
- Fraktale: Mandelbrot- und Julia-Mengen
- Geometrie: Konforme Abbildungen und Transformationen
|
|