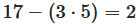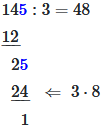Division with remainder

Division with remainder is the division of two integers, which produces a quotient and a remainder.

If a natural number \(a\) divides by a natural number \(b\), then it is calculated how many times the number \(b\) is contained in \(a\). The result is the quotient \(q\) and possibly a remainder \(r\).

We can write

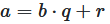
Example  

The remainder is therefore the difference between the dividend and the largest multiple of the divisor

A remainder arises only if the dividend is not a multiple of the divisor. In other words, if the dividend is not divisible by the divisor.

Division and negative numbers

Dividing numbers with different signs gets the following results.

Example

To divide numbers, you write them side by side with the division symbol in between.

Divide the first digit of the left number by the right number. If that doesn't work, add the second digit on the left, here 14.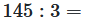

Now multiply the result by the right number, write the product under the digits used in the left number and form the difference.

Then you pull the next digit of the left number down and calculate again.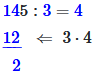

The result is 48 remainder 1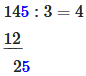