Division mit Rest
Schriftliche Division und die Rolle des Restes
Die Division mit Rest ist eine grundlegende arithmetische Operation, die zeigt, wie oft eine Zahl in eine andere passt und was dabei überbleibt. Sie ist essentiell für das Verständnis von Modulo-Operationen, Teilbarkeit und vielen praktischen Anwendungen in Mathematik, Informatik und Physik.
Grundlagen der Division mit Rest
Wenn man eine natürliche Zahl a (den Dividend) durch eine natürliche Zahl b (den Divisor) dividiert, erhält man:
- Quotient q: Wie oft der Divisor in den Dividend passt
- Rest r: Was nach der vollständigen Division übrig bleibt
Für Dividend a, Divisor b, Quotient q und Rest r gilt:
a = b · q + r, wobei 0 ≤ r < b
Der Rest muss immer kleiner als der Divisor sein und nicht-negativ.
Praktisches Beispiel
Aufgabe: 17 ÷ 5
- Die 5 passt 3-mal in die 17 (weil 5 · 3 = 15)
- Rest: 17 - 15 = 2
- Ergebnis: 17 = 5 · 3 + 2
- Schreibweise: 17 ÷ 5 = 3 Rest 2
Zusammenhang zwischen den Komponenten
Der Rest ist die Differenz zwischen dem Dividend und dem größten Vielfachen des Divisors, das nicht größer als der Dividend ist:
Beispiel:
r = 17 - (5 · 3) = 17 - 15 = 2
Ein Rest ergibt sich nur dann, wenn der Dividend kein Vielfaches des Divisors ist. Wenn der Dividend durch den Divisor teilbar ist, ist der Rest 0.
Beispiel: 15 ÷ 5 = 3 Rest 0 (da 15 = 5 · 3)
Schriftliche Division durchführen
Die schriftliche Division (auch Langdivision genannt) ist ein systematisches Verfahren, um große Zahlen zu dividieren. Wir werden dies Schritt für Schritt durchgehen.
Die Schritte der schriftlichen Division
Aufschreiben
Schreibe Dividend und Divisor mit dem Divisionszeichen auf
Erste Ziffer(n) nehmen
Nimm so viele Ziffern von links, bis die Zahl ≥ Divisor ist
Dividieren
Teile die Zahl durch den Divisor und schreibe das Ergebnis auf
Multiplizieren & Subtrahieren
Multipliziere das Ergebnis mit dem Divisor und subtrahiere von der Zahl
Nächste Ziffer
Hole die nächste Ziffer herunter und wiederhole ab Schritt 3
Abschluss
Wenn keine Ziffern mehr vorhanden sind, ist die Subtraktion der Rest
Beispiel: 145 ÷ 3
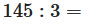
Schritt 1: Aufschreiben der Aufgabe 145 ÷ 3

Schritt 2-3: 14 ÷ 3 = 4 (da 3 · 4 = 12)
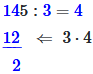
Schritt 4: 12 subtrahieren: 14 - 12 = 2
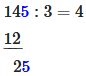
Schritt 5: Nächste Ziffer 5 herunterholen: ergibt 25
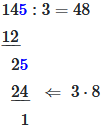
Schritt 6-7: 25 ÷ 3 = 8 (da 3 · 8 = 24); Rest: 25 - 24 = 1
145 ÷ 3 = 48 Rest 1
Verifikation: 3 · 48 + 1 = 144 + 1 = 145 ✓
Division mit negativen Zahlen
Wenn Dividend und/oder Divisor negativ sind, gelten besondere Regeln. Die Behandlung des Vorzeichens unterscheidet sich von der Multiplikation.
Vorzeichenregeln
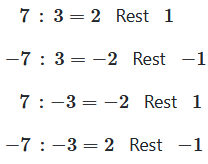
Beispiele für Division mit verschiedenen Vorzeichen
| Dividend | Divisor | Quotient Vorzeichen | Beispiel |
|---|---|---|---|
| positiv | positiv | positiv | 7 ÷ 3 = 2 Rest 1 |
| negativ | positiv | negativ | -7 ÷ 3 = -3 Rest 2 |
| positiv | negativ | negativ | 7 ÷ (-3) = -3 Rest 1 |
| negativ | negativ | positiv | -7 ÷ (-3) = 2 Rest -1 |
Der Rest muss immer nicht-negativ sein und kleiner als der Betrag des Divisors. Dies kann zu kontraintuativen Ergebnissen führen, wenn mit negativen Zahlen gearbeitet wird.
Beispiel: -7 ÷ 3 = -3 Rest 2 (nicht -2 Rest -1), weil -7 = 3 · (-3) + 2 gelten muss mit 0 ≤ 2 < 3
Praktische Anwendungen
Mathematik
- Teilbarkeit: Prüfung, ob eine Zahl durch eine andere teilbar ist
- Primzahltest: Bestimmung der Teilbarkeit durch Primzahlen
- Restklassen: Modulo-Arithmetik in der Zahlentheorie
- GCD-Berechnung: Euklidischer Algorithmus verwendet Division mit Rest
Informatik
- Modulo-Operator (%): Berechnung des Restes in Programmiersprachen
- Hash-Funktionen: Verteilung auf begrenzte Bereiche
- Array-Indexierung: Zirkuläre Indizierung mit Modulo
- Kryptografie: RSA und andere Algorithmen nutzen Modulo-Arithmetik
Alltag
- Verteilung: Wie viele Gruppen und was bleibt übrig
- Wechselgeld: Berechnung der Restbeträge
- Zeitberechnung: Umrechnung zwischen Einheiten (z.B. Minuten zu Stunden)
- Kalender: Bestimmung des Wochentages mit Modulo-7
Zusammenfassung wichtiger Konzepte
| Konzept | Definition | Schreibweise |
|---|---|---|
| Dividend | Die Zahl, die geteilt wird | a in "a ÷ b" |
| Divisor | Die Zahl, durch die geteilt wird | b in "a ÷ b" |
| Quotient | Das Ergebnis der Division (ohne Rest) | q in "a = b · q + r" |
| Rest | Was nach der Division übrig bleibt | r in "a = b · q + r" |
| Divisionsgleichung | a = b · q + r mit 0 ≤ r < b | Euklidscher Algorithmus |
| Modulo-Operation | Berechnung nur des Restes | a mod b = r |
Tipps zum Lernen und Rechnen
- Immer überprüfen: Berechne b · q + r und vergleiche mit a
- Rest beachten: Der Rest muss immer kleiner als der Divisor sein
- Stellenweise arbeiten: Nimm schrittweise Ziffern herunter
- Größenabschätzung: Schätze den Quotient grob ab
- Teilbarkeit nutzen: Erkenne Muster bei Divisibilität
Nach jeder Division mit Rest solltest du überprüfen:
a = b · q + r
Beispiel: Bei 145 ÷ 3 = 48 Rest 1
Überprüfung: 3 · 48 + 1 = 144 + 1 = 145 ✓
Online-Tool
Teste dein Verständnis mit unserem interaktiven Rechner:
|
|