Modulo

Der Rest einer Division und seine Anwendungen

Modulo bezeichnet den Rest einer Division mit ganzen Zahlen. Das Modulo ist eine fundamentale Operation in Mathematik und Informatik und wird in den meisten Programmiersprachen als eigenständiger Operator bereitgestellt. In der Mathematik entspricht es dem Rest aus der Division mit Rest, die wir unter Division mit Rest behandelt haben.

Definition und Notation

Modulo ist eine mathematische Operation, die den Rest einer Divisionsoperation berechnet.

Definition:

Für zwei ganze Zahlen a und b (b ≠ 0) ist a mod b der Rest der Division von a durch b.

a mod b = r, wobei a = b · q + r und 0 ≤ r < |b|

Notation und Schreibweise

Mathematische Notation:
a mod b = r

Programmiersprachen:
Python, Java, C++: a % b
Ruby, JavaScript, PHP: a % b
Visual Basic, Pascal: a mod b

Praktisches Beispiel

Aufgabe: 17 mod 5

17 ÷ 5 = 3 Rest 2
Verifikation: 5 · 3 + 2 = 15 + 2 = 17 ✓
Ergebnis: 17 mod 5 = 2

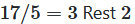
Grafische Darstellung: 17 mod 5 = 2

Eigenschaften des Modulo

Nicht-negativer Rest

Das Ergebnis ist immer nicht-negativ: 0 ≤ a mod b < |b|

Teilbarkeit

a mod b = 0 genau dann, wenn a durch b teilbar ist

Symmetrie

Das Modulo mit derselben Zahl wiederholt: a mod b mod b = a mod b

Verkettung

(a + c) mod b = ((a mod b) + (c mod b)) mod b

Multiplikation

(a · c) mod b = ((a mod b) · (c mod b)) mod b

Identität

a mod 1 = 0 für alle ganzen Zahlen a

Modulo mit positiven Zahlen

Bei positiven Dividenden und Divisoren ist die Modulo-Operation sehr einfach zu verstehen.

Beispiele mit positiven Zahlen

7 mod 3 = 1 (da 7 = 3 · 2 + 1)
10 mod 4 = 2 (da 10 = 4 · 2 + 2)
15 mod 5 = 0 (da 15 = 5 · 3 + 0, 15 ist teilbar)
23 mod 7 = 2 (da 23 = 7 · 3 + 2)
100 mod 6 = 4 (da 100 = 6 · 16 + 4)

Modulo mit negativen Zahlen

Wenn Dividend und/oder Divisor negativ sind, werden die Ergebnisse komplexer. Verschiedene Programmiersprachen handhaben negative Zahlen unterschiedlich bei der Modulo-Operation.

Mathematische Definition (Euklidischer Algorithmus)

In der Mathematik ist das Ergebnis immer nicht-negativ und im Bereich [0, |b|):

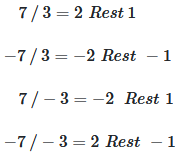
Beispiele für Modulo mit verschiedenen Vorzeichen

a	b	Mathematisch (a mod b)	Programmierung (oft anders!)	Erklärung
7	3	1	1	Beide positiv
-7	3	2	-1 oder 2	a negativ: Ergebnis nicht-negativ
7	-3	1	1 oder -2	b negativ: abhängig vom System
-7	-3	2	-1 oder 2	Beide negativ

Programmiersprachen behandeln negative Modulo unterschiedlich!

Es gibt zwei häufige Konventionen:

Truncated Division (C, Java, C++): Ergebnis hat Vorzeichen des Dividenden
Floored Division (Python, Ruby): Ergebnis hat Vorzeichen des Divisors

Beispiel: -7 mod 3
C/Java: -1 (Vorzeichen von -7)
Python: 2 (Vorzeichen von 3, immer 0 ≤ r < |b|)

Praktische Anwendungen des Modulo

Mathematik und Zahlentheorie

Teilbarkeit: a mod b = 0 bedeutet, dass a durch b teilbar ist
Primzahltest: Schnelle Überprüfung von Teilbarkeit
Größter gemeinsamer Teiler (GCD): Euklidischer Algorithmus nutzt Modulo
Restklassen: Grundlage der Modularen Arithmetik

Informatik und Programmierung

Hash-Funktionen: Verteilung auf begrenzte Array-Indizes
Zirkuläre Arrays: Wrap-Around bei Grenzwerten
Scheduling: Round-Robin Zuteilung von Ressourcen
Datenstruktur-Operationen: Prüfung von Potenzahl-Bedingungen

Alltägliche Anwendungen

Kalendersystem: Bestimmung des Wochentages (mod 7)
Zeitberechnung: Umwandlung zwischen Einheiten (Stunden zu Minuten)
Verteilung: Wie viele Gruppen und was bleibt übrig
Kontrolltechniken: Prüfsummen und Checksummen
Spielelogik: Rundenreihenfolge in Spielen

Modulo in Kryptografie und Sicherheit

Modulo-Arithmetik ist fundamental für viele Kryptografische Verfahren.

Kryptografische Anwendungen

RSA-Verschlüsselung: Modulo mit großen Primzahlen für Sicherheit
SHA / MD5 Hash: Modulo zur Erzeugung von Hash-Werten
Pseudozufallszahlen: Lineare Kongruenz-Generatoren nutzen Modulo
Digitale Signaturen: Verifikation durch modulare Exponentiation

Warum Modulo in der Kryptografie?

Modulo-Operationen mit großen Primzahlen erzeugen mathematische Probleme, die sehr schwierig zu lösen sind (z.B. diskrete Logarithmen). Dies bildet die Grundlage für sichere Verschlüsselung.

Modulo in verschiedenen Programmiersprachen

Python

print(17 % 5)    # Output: 2

print(-7 % 3)    # Output: 2 (nicht -1!)

print(10 % 4)    # Output: 2

x = 15

if x % 2 == 0:

    print("x ist gerade")

else:

    print("x ist ungerade")

JavaScript

console.log(17 % 5);    // Output: 2

console.log(-7 % 3);    // Output: -1

console.log(10 % 4);    // Output: 2

const x = 15;

if (x % 2 === 0) {

    console.log("x ist gerade");

} else {

    console.log("x ist ungerade");

}

Java / C++

System.out.println(17 % 5);    // Output: 2

System.out.println(-7 % 3);    // Output: -1

System.out.println(10 % 4);    // Output: 2

int x = 15;

if (x % 2 == 0) {

    System.out.println("x ist gerade");

} else {

    System.out.println("x ist ungerade");

}

Zusammenfassung und Vergleich

Konzept	Definition	Symbol	Beispiel
Modulo (Mathematik)	Rest einer Division (nicht-negativ)	a mod b	17 mod 5 = 2
Modulo (Programmierung)	Rest einer Division (sprachabhängig)	a % b	17 % 5 = 2
Gerade Zahl	Teilbar durch 2	a mod 2 = 0	10 mod 2 = 0
Ungerade Zahl	Nicht teilbar durch 2	a mod 2 = 1	11 mod 2 = 1
Teilbarkeit	Wenn Rest 0 ist	a mod b = 0	15 mod 5 = 0
Restklasse	Äquivalenzklasse unter Modulo	a ≡ b (mod n)	12 ≡ 2 (mod 5)

Tipps und häufige Fehler

Nützliche Tipps:

Schnelle Geraden/Ungerade-Prüfung: Nutze a % 2
Modulo mit Divisor 1: Ergebnis ist immer 0
Modulo-Kettenregel: (a mod b) mod b = a mod b
Performance: Modulo kann teuer sein; nutze Bitshift bei Potenzen von 2
Programmiersprachen beachten: Negative Zahlen verhalten sich unterschiedlich!

Häufige Fehler:

FALSCH: Annahme, dass a mod b = b mod a | RICHTIG: a mod b ≠ b mod a (außer Spezialfälle)
FALSCH: Modulo durch 0 | RICHTIG: Modulo durch Null ist undefiniert!
FALSCH: Ignorieren von negativen Zahlen | RICHTIG: Programmiersprachen haben unterschiedliche Konventionen
FALSCH: Vergessen, dass Modulo Priorität hat | RICHTIG: In Ausdrücken korrekt klammern