Matrix Multiplication 3×3
Calculator for multiplying 3x3 matrices
Matrix Multiplication Calculator
Instructions
Enter the values of both matrices to be multiplied. Empty fields are counted as zero. Click Calculate.
Matrix Multiplication - Overview
Prerequisites
Two matrices can be multiplied if the number of columns in the left matrix is the same as the number of rows in the right matrix.
Calculation Formula
The product of a matrix is calculated by calculating the product sums of the pairs from the row vectors of the first matrix and the column vectors of the second matrix.
\(C_{ij} = \sum_{k=1}^{n} A_{ik} \cdot B_{kj}\)
Example
Calculating element C11:
\(\text{Row 1 of A} \times \text{Column 1 of B}\)
\(C_{11} = A_{11} \cdot B_{11} + A_{12} \cdot B_{21} + A_{13} \cdot B_{31}\)
Properties
- Not commutative: A × B ≠ B × A (order matters!)
- Associative: (A × B) × C = A × (B × C)
- Distributive: A × (B + C) = A × B + A × C
- Identity: A × I = I × A = A
- Dimension: (m×n) × (n×p) = (m×p)
|
|
Description of Matrix Multiplication
Fundamentals
There is a special rule for multiplication of matrices constructed in such a way that they can represent simultaneous equations using matrices.
Key Rules:
- Two matrices can be multiplied if the number of columns in the left matrix is the same as the number of rows in the right matrix.
- The product of a matrix is calculated by calculating the product sums of the pairs from the row vectors of the first matrix and the column vectors of the second matrix.
Calculation Steps
- Select a row from matrix A
- Select a column from matrix B
- Multiply corresponding elements
- Sum all the products
- Place result in the corresponding position of matrix C
Detailed Example
Step-by-Step Calculation
First element (row 1, column 1):
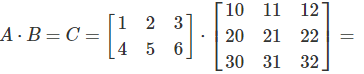
The first element of the product \(C\), is the sum of the products of each element of the first row of \(A\), and the corresponding element of the first column of \(B\).
Visual Representation:
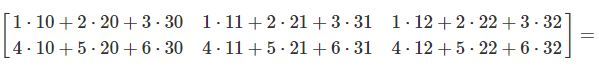
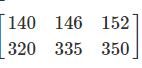
Pattern Recognition:
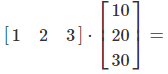
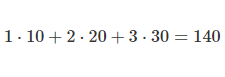
Practical Applications
Mathematics & Physics:
- Solving systems of linear equations
- Coordinate transformations
- Quantum mechanics calculations
- Graph theory problems
Engineering & Computer Science:
- 3D graphics transformations
- Neural networks (deep learning)
- Robotics (pose transformations)
- Computer vision algorithms
Important Note
Matrix multiplication is NOT commutative! This means A × B ≠ B × A. The order of multiplication is crucial. For example, if you multiply a 3×2 matrix by a 2×3 matrix, you get a 3×3 result. But if you reverse the order, you get a 2×2 result - completely different!
|
|