Matrizenmultiplikation
Multiplikation von Matrizen mit Beispielen und Regeln
Mit Matrizen kann genauso gerechnet werden wie mit normalen Zahlen. Die Multiplikation von Matrizen ist eine der wichtigsten Operationen und folgt speziellen Regeln, die für die Anwendung in linearen Gleichungssystemen konstruiert wurden.
Die Matrizenmultiplikation ist komplexer als Addition oder Subtraktion und erfordert sorgfältige Aufmerksamkeit auf die Dimensionen und die richtige Berechnung der Elemente.
Die Dimensionsregel für Multiplikation
Nicht alle Matrizenpaare können miteinander multipliziert werden. Die zentrale Regel ist:
- Spalten der ersten Matrix = Zeilen der zweiten Matrix
- Notation: A (m × n) kann mit B (n × p) multipliziert werden
- Ergebnis: Die Produktmatrix C hat die Dimension m × p
- Merksatz: (m × n) · (n × p) = (m × p)
Beispiele: Welche Matrizen können multipliziert werden?
Matrix A: 2 × 3 (2 Zeilen, 3 Spalten)
Matrix B: 3 × 2 (3 Zeilen, 2 Spalten)

Grund: Spalten von A (3) = Zeilen von B (3) → Multiplikation möglich ✓
Ergebnis: C wird 2 × 2 Matrix (2 Zeilen, 2 Spalten)
Matrix A: 2 × 3 (2 Zeilen, 3 Spalten)
Matrix B: 2 × 2 (2 Zeilen, 2 Spalten)

Grund: Spalten von A (3) ≠ Zeilen von B (2) → Multiplikation NICHT möglich ✗
Die Multiplikationsmethode: Zeile × Spalte
Das Produkt wird berechnet, indem man Skalarprodukte aus Zeilenvektoren der ersten Matrix und Spaltenvektoren der zweiten Matrix bildet.
c_ij = a_i1 · b_1j + a_i2 · b_2j + ... + a_in · b_nj
Das Element c_ij entsteht durch das Skalarprodukt der i-ten Zeile von A mit der j-ten Spalte von B.
Das Skalarprodukt (Dot Product)
Ein Skalarprodukt ist die Summe der Produkte entsprechender Elemente aus einem Vektor mit einem anderen:
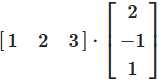
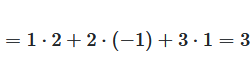
Abbildung 1: Berechnung eines Skalarprodukts
Beispiel: Skalarprodukt berechnen
Detaillierte Beispiele
Beispiel 1: 2 × 2 Matrizen multiplizieren
Allgemeine Formel für 2 × 2 Matrizen
Beispiel 2: 2 × 2 Matrizen mit Zahlen
Konkretes Zahlenbeispiel
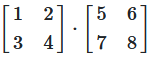
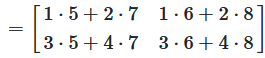
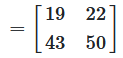
Abbildung 2: Visuelle Darstellung der 2 × 2 Matrizenmultiplikation
Beispiel 3: Größere Matrizen (2×3) × (3×4)
Multiplikation mit unterschiedlichen Dimensionen
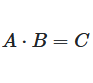
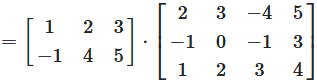

Abbildung 3: Matrizenmultiplikation mit größeren Matrizen
Eigenschaften der Matrizenmultiplikation
Assoziativität
(A · B) · C = A · (B · C)
Klammern können verschoben werden
Distributivität
A · (B + C) = A · B + A · C
Ausmultiplizieren möglich
Nicht kommutativ
A · B ≠ B · A
Reihenfolge ist entscheidend
Mit Einheitsmatrix
A · I = I · A = A
Neutrale Element
Wichtige Hinweise und Besonderheiten
- Nicht kommutativ: A · B ≠ B · A! Die Reihenfolge ist entscheidend
- Dimensionen: Spalten(A) muss = Zeilen(B) sein
- Ergebnis-Dimension: (m × n) · (n × p) = (m × p)
- Zeile × Spalte: Element c_ij = i-te Zeile von A · j-te Spalte von B
- Skalarprodukt: Multiplikation und Addition kombiniert
- Dimensionsprüfung: Immer vor der Multiplikation überprüfen!
- Reihenfolge zählt: A · B ≠ B · A (nicht kommutativ)
- Element-weise: Jedes Element ist ein Skalarprodukt
- Aufwand: Matrizenmultiplikation ist rechenintensiv!
Zusammenfassung
| Aspekt | Beschreibung |
|---|---|
| Dimensionsbedingung | Spalten(A) = Zeilen(B) |
| Ergebnis-Dimension | (m × n) · (n × p) = (m × p) |
| Berechnung | c_ij = Σ a_ik · b_kj (Zeile × Spalte) |
| Kommutativ | Nein: A · B ≠ B · A |
| Assoziativ | Ja: (A · B) · C = A · (B · C) |
| Distributiv | Ja: A · (B + C) = A · B + A · C |
Tipps und häufige Fehler
- Dimensions-Matrix zeichnen: Visualisieren Sie die Dimensionen (m×n)·(n×p)
- Systematisch arbeiten: Element für Element, Zeile für Zeile berechnen
- Skalarproduke sorgfältig: Alle Multiplikationen addieren, nicht vergessen
- Reihenfolge überprüfen: A·B ≠ B·A! Zuerst prüfen, ob möglich
- Papier nutzen: Große Matrizen erfordern sorgfältige Notation
- FALSCH: Dimensionsregel ignorieren | RICHTIG: Spalten(A) = Zeilen(B)!
- FALSCH: A · B = B · A annehmen | RICHTIG: Nicht kommutativ!
- FALSCH: Element-weise Multiplikation (wie bei Addition) | RICHTIG: Zeile × Spalte Skalarprodukt
- FALSCH: Produkte vergessen zu addieren | RICHTIG: Alle Produkte summieren
Online-Rechner
Teste deine Matrizenmultiplikation mit unserem interaktiven Online-Rechner:
|
|