Kegelstumpf Rechner
Rechner und Formeln zur Berechnung eines Kegelstumpfs
Kegelstumpf Rechner
Der Gerade Kegelstumpf
Der gerade Kegelstumpf ist ein abgeschnittener Kegel mit zwei parallelen kreisförmigen Grundflächen unterschiedlicher Größe.
Kegelstumpf Eigenschaften
Der gerade Kegelstumpf: Abgeschnittener Kegel mit zwei parallelen Kreisflächen
Kegelstumpf Struktur
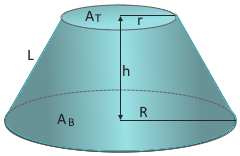
Der gerade Kegelstumpf mit zwei parallelen Kreisflächen.
Konische Mantelfläche zwischen den Grundflächen.
|
|
Was ist ein gerader Kegelstumpf?
Der gerade Kegelstumpf ist ein faszinierender Rotationskörper:
- Definition: Abgeschnittener Kegel zwischen zwei parallelen Ebenen
- Grundflächen: Zwei parallele Kreise unterschiedlicher Größe
- Mantelfläche: Konische Verbindung zwischen den Kreisen
- Achse: Senkrecht zu beiden Grundflächen
- Mantellinie: Schräge Verbindung der Kreisränder
- Symmetrie: Rotationssymmetrie um die Achse
Geometrische Eigenschaften des Kegelstumpfs
Der gerade Kegelstumpf zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Kleiner Radius (r): Radius der oberen Fläche
- Großer Radius (R): Radius der Basisfläche
- Höhe (h): Abstand zwischen den Grundflächen
- Mantellinie (L): √((R-r)² + h²)
Besondere Eigenschaften
- Frustum: Abgeschnittener Kegel (lateinisch)
- Trapez-Profil: Trapezförmiger Querschnitt
- Ähnliche Kreise: Beide Grundflächen sind ähnlich
- Konvergenz: Mantellinien treffen sich virtuell
Mathematische Beziehungen
Der gerade Kegelstumpf folgt eleganten mathematischen Gesetzen:
Volumen-Formel
Enthält R², Rr und r² Terme. Elegante Übergangsformel.
Mantelflächen-Formel
Mittlerer Umfang mal Mantellinie. Trapezflächen-Analogie.
Anwendungen des Kegelstumpfs
Kegelstümpfe finden Anwendung in verschiedenen Bereichen:
Industrie & Technik
- Trichter und Rohrleitungen
- Behälter und Tanks
- Getriebe und Kupplungen
- Ventile und Absperrungen
Architektur & Bauwesen
- Säulen und Pfeiler
- Turmstrukturen
- Dekorative Elemente
- Fundamente und Stützen
Bildung & Wissenschaft
- Geometrie-Unterricht
- Volumenberechnungen
- 3D-Modellierung
- Ingenieursmathematik
Alltag & Design
- Lampenschirme
- Vasen und Gefäße
- Möbeldesign
- Dekorative Objekte
Formeln zum Kegelstumpf
Obere Fläche (AT)
Kreisfläche der oberen Grundfläche
Basisfläche (AB)
Kreisfläche der unteren Grundfläche
Mantelhöhe (L)
Pythagoras für die schräge Mantellinie
Mantelfläche (SL)
Konische Mantelfläche zwischen den Kreisen
Langer Umfang (PL)
Umfang der großen Grundfläche
Kurzer Umfang (PS)
Umfang der kleinen Grundfläche
Oberfläche (S)
Mantelfläche plus beide Grundflächen
Volumen (V)
Kegelstumpf-Volumen mit quadratischen Termen
Berechnungsbeispiel für einen Kegelstumpf
Gegeben
Gesucht: Alle Eigenschaften des geraden Kegelstumpfs
1. Grundflächen-Berechnung
Für r = 4, R = 5:
\[A_T = r^2 \cdot \pi = 16\pi ≈ 50.27\] \[A_B = R^2 \cdot \pi = 25\pi ≈ 78.54\]Obere Fläche: 50.27, Basisfläche: 78.54
2. Mantellinie-Berechnung
Für R = 5, r = 4, h = 3:
\[L = \sqrt{(R-r)^2 + h^2}\] \[L = \sqrt{1^2 + 3^2} = \sqrt{10}\] \[L ≈ 3.16\]Die Mantellinie beträgt etwa 3.16 Längeneinheiten
3. Volumen-Berechnung
Für R = 5, r = 4, h = 3:
\[V = \frac{\pi \cdot h}{3}(R^2 + Rr + r^2)\] \[V = \frac{\pi \cdot 3}{3}(25 + 20 + 16)\] \[V = 61\pi ≈ 191.64\]Das Volumen beträgt etwa 191.64 Volumeneinheiten
4. Oberfläche-Berechnung
Mantelfläche + Grundflächen:
\[S_L = \pi(R+r)L = 9\pi \cdot 3.16 ≈ 89.30\] \[S = S_L + A_T + A_B\] \[S ≈ 89.30 + 50.27 + 78.54 ≈ 218.11\]Die Gesamtoberfläche beträgt etwa 218.11 Flächeneinheiten
5. Der perfekte Kegelstumpf
Der gerade Kegelstumpf mit perfekter Rotationssymmetrie
Der gerade Kegelstumpf: Eleganz der abgeschnittenen Geometrie
Der gerade Kegelstumpf ist ein faszinierender Rotationskörper, der die elegante Verbindung zwischen zwei parallelen Kreisflächen unterschiedlicher Größe darstellt. Entstanden durch das Abschneiden eines Kegels mit einer zur Basis parallelen Ebene, vereint der Kegelstumpf die Eigenschaften sowohl des vollständigen Kegels als auch des Zylinders. Seine mathematische Schönheit zeigt sich in den komplexeren, aber dennoch eleganten Formeln, die quadratische Terme für Radius und gemischte Produkte enthalten und somit eine reichere geometrische Struktur widerspiegeln als einfache Rotationskörper.
Die Geometrie der Stufen
Der gerade Kegelstumpf demonstriert die Eleganz der gestuften Rotation:
- Frustum-Struktur: Klassische "abgeschnittene" Form
- Trapez-Profil: Charakteristische trapezförmige Seitenansicht
- Duale Kreisflächen: Zwei parallele, ähnliche Kreise
- Konische Mantelfläche: Verbindung zwischen den Kreisen
- Pythagoras-Beziehung: L² = (R-r)² + h² für die Mantellinie
- Rotationssymmetrie: Vollständige 360°-Symmetrie
- Praktische Vielseitigkeit: Ideal für technische Anwendungen
Mathematische Komplexität
Volumen-Sophistication
Die Kegelstumpf-Volumenformel mit R², Rr und r² Termen zeigt elegante mathematische Übergänge zwischen verschiedenen Geometrien.
Mantelflächen-Harmonie
Die Mantelfläche π(R+r)L verwendet den mittleren Umfang, eine geniale Vereinfachung der komplexen konischen Oberfläche.
Praktische Überlegenheit
Kegelstümpfe bieten strukturelle Stabilität bei optimaler Materialnutzung – perfekt für technische Anwendungen.
Ästhetische Balance
Die harmonische Proportion zwischen zwei Kreisflächen erzeugt visuell ansprechende und funktionale Formen.
Zusammenfassung
Der gerade Kegelstumpf repräsentiert die perfekte Balance zwischen geometrischer Komplexität und praktischer Anwendbarkeit. Seine eleganten Formeln mit quadratischen und gemischten Termen spiegeln die reichere Struktur wider, die durch die Verbindung zweier unterschiedlicher Kreisflächen entsteht. Von industriellen Trichtern bis zu architektonischen Säulen zeigt der Kegelstumpf seine Vielseitigkeit in unzähligen Anwendungen. Als Brücke zwischen der einfachen Kegelgeometrie und komplexeren Rotationskörpern demonstriert er, wie mathematische Eleganz und praktische Funktionalität in perfekter Harmonie vereint werden können. Seine einzigartige Fähigkeit, strukturelle Stabilität mit optimaler Materialverteilung zu kombinieren, macht ihn zu einem der wichtigsten Körper der angewandten Geometrie.
|
|
|
|