Spitze Säule Rechner
Rechner und Formeln zur Berechnung einer spitzen Säule
Spitze Säule Rechner
Die Spitze Säule
Die spitze Säule ist ein zusammengesetzter Rotationskörper aus einem Kegelstumpf mit aufgesetztem Kegel.
Spitze Säule Eigenschaften
Die spitze Säule: Zusammengesetzter Körper aus Kegelstumpf und Kegel
Spitze Säule Struktur
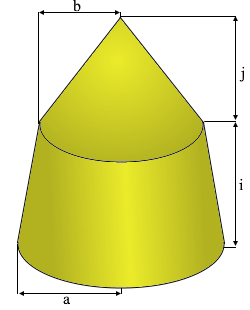
Die spitze Säule als zusammengesetzter Rotationskörper.
Kegelstumpf mit aufgesetztem Kegel.
|
|
Was ist eine spitze Säule?
Die spitze Säule ist ein faszinierender zusammengesetzter Rotationskörper:
- Definition: Kegelstumpf mit aufgesetztem Kegel
- Basis: Große kreisförmige Grundfläche
- Übergang: Mittlerer Kreis zwischen beiden Teilen
- Spitze: Kegelförmiger oberer Abschluss
- Symmetrie: Rotationssymmetrie um die Achse
- Struktur: Zwei verbundene Rotationskörper
Geometrische Eigenschaften der spitzen Säule
Die spitze Säule zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Unterer Radius (a): Radius der Basisfläche
- Übergang Radius (b): Radius am Übergang
- Kegelstumpf Höhe (i): Höhe des unteren Teils
- Kegel Höhe (j): Höhe des oberen Teils
Besondere Eigenschaften
- Zusammengesetzt: Zwei Rotationskörper vereint
- Kontinuierlich: Nahtloser Übergang
- Vielseitig: Verschiedene Proportionen möglich
- Stabil: Breite Basis, spitze Oberseite
Mathematische Beziehungen
Die spitze Säule folgt komplexen mathematischen Gesetzen:
Volumen-Formel
Summe aus Kegelstumpf- und Kegelvolumen. Komplexe quadratische Terme.
Mantelflächen-Formel
Kegelstumpf-Mantel plus Kegel-Mantel. Pythagoras für Mantellinien.
Anwendungen der spitzen Säule
Spitze Säulen finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Säulen und Pfeiler
- Türme und Spitzen
- Obelisken und Monumente
- Dekorative Bauelemente
Industrie & Technik
- Behälter und Tanks
- Kühltürme
- Antennen und Masten
- Maschinenbauteile
Bildung & Wissenschaft
- Geometrie-Unterricht
- Zusammengesetzte Körper
- 3D-Modellierung
- Mathematische Anwendungen
Kunst & Design
- Skulpturen
- Vasen und Gefäße
- Möbeldesign
- Dekorative Objekte
Formeln zur Spitzen Säule
Basisfläche (A)
Kreisfläche der unteren Grundfläche
Oberfläche (S)
Basisfläche plus Mantelfläche
Mantelfläche (L)
Komplexe Formel für Kegelstumpf-Mantel plus Kegel-Mantel
Volumen (V)
Kegelstumpf-Volumen plus Kegel-Volumen
Berechnungsbeispiel für eine spitze Säule
Gegeben
Gesucht: Alle Eigenschaften der spitzen Säule
1. Basisfläche-Berechnung
Für a = 4:
\[A = a^2 \cdot \pi\] \[A = 4^2 \cdot \pi = 16\pi\] \[A ≈ 50.27\]Die Basisfläche beträgt etwa 50.27 Flächeneinheiten
2. Kegelstumpf-Volumen
Kegelstumpf-Teil:
\[V_{Stumpf} = \frac{\pi \cdot i}{3}(a^2 + ab + b^2)\] \[V_{Stumpf} = \frac{\pi \cdot 4}{3}(16 + 12 + 9)\] \[V_{Stumpf} = \frac{148\pi}{3} ≈ 154.99\]Das Kegelstumpf-Volumen beträgt etwa 154.99
3. Kegel-Volumen
Kegel-Teil:
\[V_{Kegel} = \frac{\pi \cdot b^2 \cdot j}{3}\] \[V_{Kegel} = \frac{\pi \cdot 9 \cdot 3}{3}\] \[V_{Kegel} = 9\pi ≈ 28.27\]Das Kegel-Volumen beträgt etwa 28.27
4. Gesamt-Volumen
Gesamtvolumen:
\[V = V_{Stumpf} + V_{Kegel}\] \[V ≈ 154.99 + 28.27\] \[V ≈ 183.26\]Das Gesamtvolumen beträgt etwa 183.26 Volumeneinheiten
5. Die perfekte spitze Säule
Die spitze Säule als eleganter zusammengesetzter Rotationskörper
Die spitze Säule: Eleganz der zusammengesetzten Geometrie
Die spitze Säule repräsentiert eine der elegantesten Formen der zusammengesetzten Rotationskörper und vereint die strukturelle Stabilität eines Kegelstumpfs mit der ästhetischen Vollendung einer Kegelspitze. Diese bemerkenswerte geometrische Konstruktion entsteht durch die harmonische Verbindung zweier fundamentaler Rotationskörper - einem Kegelstumpf als stabiler Basis und einem Kegel als eleganter Krönung. Die mathematische Komplexität der spitzen Säule zeigt sich in den anspruchsvollen Formeln, die sowohl quadratische Terme als auch Wurzelausdrücke kombinieren und damit die reiche geometrische Struktur dieses zusammengesetzten Körpers widerspiegeln.
Die Geometrie der Komposition
Die spitze Säule demonstriert die Kraft der geometrischen Komposition:
- Duale Struktur: Kegelstumpf-Basis mit Kegel-Spitze
- Kontinuierlicher Übergang: Nahtlose Verbindung am Übergangsradius
- Stabile Basis: Breite Grundfläche für strukturelle Integrität
- Elegante Spitze: Kegelförmiger Abschluss für ästhetische Vollendung
- Rotationssymmetrie: Vollständige 360°-Symmetrie um die Achse
- Proportionale Harmonie: Ausgewogenes Verhältnis der Komponenten
- Vielseitige Gestaltung: Verschiedene Proportionen möglich
Mathematische Sophistication
Volumen-Komposition
Die Volumenformel vereint Kegelstumpf- und Kegelvolumen in einem eleganten Ausdruck mit gemischten quadratischen Termen.
Mantelflächen-Integration
Die komplexe Mantelflächenformel kombiniert zwei Pythagorean-Terme für die unterschiedlichen Mantellinien.
Strukturelle Überlegenheit
Die Kombination aus stabiler Basis und spitzer Krone bietet optimale strukturelle und ästhetische Eigenschaften.
Architektonische Perfektion
Von antiken Säulen bis zu modernen Türmen - die spitze Säule verkörpert zeitlose architektonische Eleganz.
Zusammenfassung
Die spitze Säule steht als Symbol für die Perfektion der zusammengesetzten Geometrie und die Harmonie architektonischer Proportionen. Ihre elegante Kombination aus struktureller Stabilität und ästhetischer Vollendung macht sie zu einer der wertvollsten Formen der angewandten Geometrie. Von klassischen Monumenten bis zu modernen Industrieanwendungen zeigt die spitze Säule ihre Vielseitigkeit und zeitlose Schönheit. Als Brücke zwischen der reinen Mathematik und der praktischen Anwendung demonstriert sie, wie komplexe geometrische Beziehungen zu funktionalen und ästhetisch ansprechenden Strukturen führen können. Ihre mathematische Sophistication, verkörpert in den eleganten Formeln für Volumen und Mantelfläche, spiegelt die reiche geometrische Struktur wider, die durch die harmonische Vereinigung zweier fundamentaler Rotationskörper entsteht.
|
|
|
|