Elliptischer Kegelstumpf Rechner
Rechner und Formeln zur Berechnung eines elliptischen Kegelstumpfs
Elliptischer Kegelstumpf Rechner
Der Elliptische Kegelstumpf
Der elliptische Kegelstumpf ist ein abgeschnittener Kegel mit elliptischen Grundflächen.
Elliptischer Kegelstumpf Eigenschaften
Der abgeschnittene elliptische Kegel: Zwei elliptische Flächen mit verschiedenen Größen
Kegelstumpf Struktur
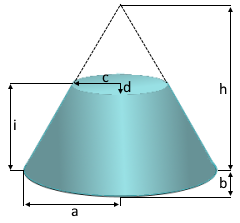
Der elliptische Kegelstumpf mit zwei Ellipsen.
Abgeschnittener Kegel mit komplexer Form.
|
|
Was ist ein elliptischer Kegelstumpf?
Der elliptische Kegelstumpf ist ein komplexer geometrischer Körper:
- Definition: Abgeschnittener elliptischer Kegel
- Zwei Ellipsen: Untere und obere Grundfläche
- Parameter: Vier Halbachsen (a, b, c, d)
- Höhen: Gesamthöhe h und Stumpfhöhe i
- Proportional: Obere Ellipse proportional kleiner
- Mantelfläche: Komplexe Berechnung
Geometrische Eigenschaften des elliptischen Kegelstumpfs
Der elliptische Kegelstumpf zeigt komplexe geometrische Eigenschaften:
Grundparameter
- Untere Halbachsen: a, b (größere Ellipse)
- Obere Halbachsen: c, d (kleinere Ellipse)
- Gesamthöhe: h (ursprünglicher Kegel)
- Stumpfhöhe: i (verbleibender Teil)
Besondere Eigenschaften
- Proportionalität: c/a = d/b = j/h
- Zwei Ellipsen: Untere und obere Grundfläche
- Abgeschnitten: Teil des ursprünglichen Kegels
- Praktisch: Häufig in Technik und Architektur
Mathematische Beziehungen
Der elliptische Kegelstumpf folgt komplexen mathematischen Gesetzen:
Volumen-Formel
Volumen = Großer Kegel - Kleiner Kegel.
Mantelflächen-Formel
Näherungsformel für praktische Anwendungen.
Anwendungen des elliptischen Kegelstumpfs
Elliptische Kegelstümpfe finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Säulenkapitelle und -basen
- Moderne Brückenbauten
- Dekorative Strukturelemente
- Kuppel- und Dachkonstruktionen
Wissenschaft & Technik
- Behälter und Tanks
- Optische Komponenten
- Maschinenbau-Teile
- Strömungstechnik
Bildung & Lehre
- Geometrie-Unterricht
- Komplexe 3D-Formen
- Proportionalitäts-Studien
- CAD-Anwendungen
Kunst & Design
- Skulpturen und Installationen
- Vasen und Gefäße
- Industriedesign
- Architektonische Details
Formeln zum elliptischen Kegelstumpf
Abgeschnittene Höhe (j)
Höhe des abgeschnittenen Teils
Basisfläche (A)
Elliptische untere Grundfläche
Große obere Halbachse (c)
Proportional zur unteren Halbachse
Kleine obere Halbachse (d)
Proportional zur unteren Halbachse
Volumen (V)
Differenz zwischen großem und kleinem Kegel
Mantelfläche (M) - Näherungsformel
Approximation der komplexen Mantelfläche
Oberfläche (S)
\[A_{oben} = c \cdot d \cdot π\]
Untere Fläche + Mantelfläche + obere Fläche
Berechnungsbeispiel für einen elliptischen Kegelstumpf
Gegeben
Gesucht: Alle Eigenschaften des elliptischen Kegelstumpfs
1. Abgeschnittene Höhe
Für h = 6, i = 4:
\[j = h - i = 6 - 4 = 2\]Die abgeschnittene Höhe beträgt 2 Einheiten
2. Obere Halbachsen
Für a = 3, b = 2, j = 2, h = 6:
\[c = \frac{3 \cdot 2}{6} = 1\] \[d = \frac{2 \cdot 2}{6} = \frac{2}{3} ≈ 0.67\]Obere Halbachsen: c = 1, d ≈ 0.67
3. Basisflächen-Berechnung
Untere Fläche:
\[A = 3 \cdot 2 \cdot π = 6π ≈ 18.85\]Obere Fläche:
\[A_{oben} = 1 \cdot \frac{2}{3} \cdot π ≈ 2.09\]Untere Fläche ≈ 18.85, obere Fläche ≈ 2.09
4. Volumen-Berechnung
Für alle Parameter:
\[V = \frac{π}{3} \cdot (6 \cdot 3 \cdot 2 - 2 \cdot 1 \cdot \frac{2}{3})\] \[V = \frac{π}{3} \cdot (36 - \frac{4}{3})\] \[V ≈ \frac{π}{3} \cdot 34.67 ≈ 36.3\]Das Volumen beträgt etwa 36.3 Volumeneinheiten
5. Zusammenfassung der Ergebnisse
Der elliptische Kegelstumpf mit proportional verkleinerter oberer Ellipse
Hinweis zur Proportionalität
Die oberen Halbachsen stehen in direkter Proportion zu den unteren Halbachsen. Das Verhältnis c/a = d/b = j/h bleibt konstant. In unserem Beispiel: c/a = 1/3 = d/b = (2/3)/2 = j/h = 2/6 = 1/3. Diese Proportionalität ist charakteristisch für alle Kegelstümpfe und ermöglicht die einfache Berechnung der oberen Dimensionen aus den unteren.
Der elliptische Kegelstumpf: Komplexität in der Praxis
Der elliptische Kegelstumpf ist ein faszinierender geometrischer Körper, der die Komplexität der elliptischen Geometrie mit der praktischen Anwendbarkeit abgeschnittener Formen verbindet. Als Kombination aus elliptischer Basis und Kegelstumpf-Geometrie entsteht eine einzigartige Struktur mit zwei elliptischen Grundflächen unterschiedlicher Größe, die durch eine komplexe Mantelfläche verbunden sind. Die mathematische Herausforderung liegt in der präzisen Berechnung der Proportionalitäten und der Näherung der Mantelfläche, während die praktische Bedeutung in zahlreichen technischen und architektonischen Anwendungen liegt.
Die Geometrie der doppelten Ellipse
Der elliptische Kegelstumpf zeigt die Komplexität mehrschichtiger Geometrie:
- Doppelte Ellipsen: Zwei elliptische Grundflächen mit proportionalen Dimensionen
- Proportionalität: Konstantes Verhältnis zwischen oberen und unteren Halbachsen
- Abgeschnittene Form: Praktische Anwendbarkeit durch flache Oberseite
- Komplexe Mantelfläche: Erfordert Näherungsformeln für praktische Berechnungen
- Vier Parameter: Zwei Halbachsen-Paare definieren die vollständige Form
- Höhen-Beziehung: Gesamthöhe und Stumpfhöhe bestimmen die Proportionen
- Vielseitigkeit: Ideal für technische und architektonische Anwendungen
Mathematische Herausforderungen
Proportionalitäts-Gesetze
Die mathematische Schönheit liegt in den einfachen Proportionalitäts-Beziehungen, die komplexe 3D-Formen durch elementare Verhältnisse beschreiben.
Differenz-Methode
Das Volumen wird elegant durch die Differenz zweier Kegelvolumen berechnet, was die mathematische Klarheit des Konzepts unterstreicht.
Näherungs-Techniken
Die Mantelflächen-Berechnung erfordert praktische Näherungen, die die Balance zwischen Genauigkeit und Berechenbarkeit demonstrieren.
Praktische Anwendbarkeit
Die Kombination aus mathematischer Präzision und praktischer Anwendbarkeit macht den elliptischen Kegelstumpf zu einem idealen Studienobjekt.
Zusammenfassung
Der elliptische Kegelstumpf verkörpert die perfekte Synthese zwischen mathematischer Komplexität und praktischer Anwendbarkeit. Seine Struktur aus zwei proportional verbundenen Ellipsen, berechnet durch elegante Proportionalitäts-Gesetze und Differenz-Methoden, macht ihn zu einem faszinierenden Studienobjekt für Mathematiker, Ingenieure und Architekten. Von der einfachen Proportionalitäts-Berechnung bis zur komplexen Mantelflächen-Näherung bietet der elliptische Kegelstumpf ein reichhaltiges Spektrum mathematischer und praktischer Herausforderungen. Seine Anwendungen in Technik, Architektur und Design zeigen, wie mathematische Eleganz und praktischer Nutzen perfekt harmonieren können. Der elliptische Kegelstumpf bleibt ein faszinierendes Beispiel dafür, wie die Kombination mehrerer geometrischer Konzepte zu völlig neuen und äußerst nützlichen mathematischen Strukturen führen kann.
|
|
|
|