Elliptischer Kegel Rechner
Rechner und Formeln zur Berechnung eines elliptischen Kegels
Elliptischer Kegel Rechner
Der Elliptische Kegel
Der elliptische Kegel ist ein Rotationskörper mit einer elliptischen Basisfläche.
Elliptischer Kegel Eigenschaften
Der Kegel mit elliptischer Basis: Zwei verschiedene Radien definieren die Form
Elliptischer Kegel Struktur
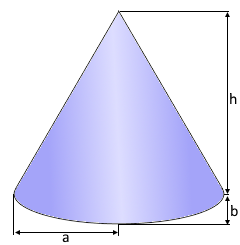
Der elliptische Kegel mit ovaler Basis.
Zwei verschiedene Radien bestimmen die Form.
|
|
Was ist ein elliptischer Kegel?
Der elliptische Kegel ist ein faszinierender geometrischer Körper:
- Definition: Kegel mit elliptischer Grundfläche
- Parameter: Zwei verschiedene Radien (a, b)
- Basis: Ellipse statt Kreis
- Mantelfläche: Komplexere Berechnung
- Symmetrie: Zwei Symmetrieachsen
- Spezialfall: a = b ergibt runden Kegel
Geometrische Eigenschaften des elliptischen Kegels
Der elliptische Kegel zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Kleiner Radius: a (kürzere Halbachse)
- Großer Radius: b (längere Halbachse)
- Höhe: h (Kegelspitze zur Basis)
- Basisfläche: A = a · b · π
Besondere Eigenschaften
- Elliptische Basis: Zwei Symmetrieachsen
- Komplexe Mantelfläche: Integral-Berechnung
- Spezialfall: a = b → runder Kegel
- Anwendungen: Optik und Technik
Mathematische Beziehungen
Der elliptische Kegel folgt komplexeren mathematischen Gesetzen:
Volumen-Formel
Das Volumen verwendet die elliptische Basisfläche.
Mantelflächen-Formel
Komplexe Berechnung über Integrale.
Anwendungen des elliptischen Kegels
Elliptische Kegel finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Ovale Kuppeln und Dächer
- Moderne Architekturformen
- Dekorative Strukturen
- Brücken-Design
Wissenschaft & Technik
- Optische Systeme
- Antennen-Design
- Strömungstechnik
- Behälterformen
Bildung & Lehre
- Geometrie-Unterricht
- Ellipsen-Studien
- Integral-Anwendungen
- 3D-Modellierung
Kunst & Design
- Skulpturen und Installationen
- Industriedesign
- Keramik und Töpferei
- Architektonische Elemente
Formeln zum elliptischen Kegel
Volumen (V)
Volumen mit elliptischer Basisfläche
Basisfläche (A)
Elliptische Grundfläche
Mantelfläche (M) - Exakte Formel
Komplexe Integral-Berechnung für exakte Mantelfläche
Mantelfläche (M) - Näherungsformel
Vereinfachte Näherungsformel (leicht unter dem exakten Wert)
Oberfläche (S)
Basisfläche plus Mantelfläche
Berechnungsbeispiel für einen elliptischen Kegel
Gegeben
Gesucht: Alle Eigenschaften des elliptischen Kegels
1. Basisflächen-Berechnung
Für a = 2, b = 3:
\[A = 2 \cdot 3 \cdot π\] \[A = 6π\] \[A ≈ 18.85\]Die Basisfläche beträgt etwa 18.85 Flächeneinheiten
2. Volumen-Berechnung
Für h = 4, A = 6π:
\[V = \frac{4 \cdot 6π}{3}\] \[V = 8π\] \[V ≈ 25.13\]Das Volumen beträgt etwa 25.13 Volumeneinheiten
3. Mantelflächen-Berechnung (Näherung)
Für a = 2, b = 3, h = 4:
\[M ≈ \frac{π}{2} \cdot \left(2\sqrt{3^2 + 4^2} + 3\sqrt{2^2 + 4^2}\right)\] \[M ≈ \frac{π}{2} \cdot \left(2\sqrt{25} + 3\sqrt{20}\right)\] \[M ≈ \frac{π}{2} \cdot \left(2 \cdot 5 + 3 \cdot 4.47\right)\] \[M ≈ \frac{π}{2} \cdot (10 + 13.41) ≈ 36.78\]Die Mantelfläche beträgt etwa 36.78 Flächeneinheiten (Näherung)
4. Oberflächen-Berechnung
Für A ≈ 18.85, M ≈ 36.78:
\[S = 18.85 + 36.78\] \[S ≈ 55.63\]Der elliptische Kegel mit ovaler Basis
Hinweis zur Mantelflächen-Berechnung
Die Mantelfläche wird hier mit der vereinfachten Näherungsformel berechnet, die etwas unter dem exakten Wert liegt. Für a = 2, b = 3, h = 4 liefert die Näherung etwa 36.78, während der exakte Wert (über das Integral berechnet) etwa 36.9 beträgt. Die Differenz ist minimal und für praktische Anwendungen vernachlässigbar.
Der elliptische Kegel: Eleganz der ovalen Form
Der elliptische Kegel ist ein faszinierender geometrischer Körper, der die Eleganz der elliptischen Form in die dritte Dimension überträgt. Im Gegensatz zum klassischen runden Kegel besitzt er eine ovale Basis, die durch zwei verschiedene Radien definiert wird. Diese scheinbar einfache Variation führt zu komplexeren mathematischen Beziehungen, insbesondere bei der Berechnung der Mantelfläche, die eine Integral-Berechnung erfordert. Die mathematische Schönheit liegt in der Verbindung von elliptischer Geometrie und Integralrechnung, die diesem Körper seine einzigartigen Eigenschaften verleiht.
Die Geometrie der elliptischen Form
Der elliptische Kegel zeigt die Komplexität der nicht-kreisförmigen Geometrie:
- Elliptische Basis: Zwei verschiedene Halbachsen definieren die ovale Form
- Doppelte Symmetrie: Zwei Symmetrieachsen in der Basisebene
- Spezialfall: Bei gleichen Radien (a = b) wird er zum runden Kegel
- Komplexe Mantelfläche: Erfordert Integral-Berechnung für exakte Werte
- Praktische Näherung: Vereinfachte Formel für alltägliche Anwendungen
- Vielseitigkeit: Ideal für optische und technische Anwendungen
- Ästhetik: Die ovale Form wirkt natürlicher und organischer
Mathematische Komplexität
Elliptische Geometrie
Die elliptische Basis führt zu eleganten, aber komplexeren Formeln, die die Schönheit der nicht-kreisförmigen Geometrie widerspiegeln.
Integral-Anwendung
Die exakte Berechnung der Mantelfläche erfordert Integralrechnung, was den elliptischen Kegel zu einem interessanten Studienobjekt macht.
Praktische Näherungen
Für praktische Anwendungen bieten Näherungsformeln ausreichende Genauigkeit bei deutlich einfacherer Berechnung.
Vielseitige Anwendungen
Von der Optik bis zur Architektur bietet die elliptische Form praktische Vorteile gegenüber runden Formen.
Zusammenfassung
Der elliptische Kegel verkörpert die perfekte Verbindung zwischen elementarer Geometrie und höherer Mathematik. Seine ovale Basis, definiert durch zwei verschiedene Radien, führt zu faszinierenden mathematischen Beziehungen, die sowohl die Eleganz der elliptischen Geometrie als auch die Macht der Integralrechnung demonstrieren. Von der einfachen Volumenberechnung bis zur komplexen Mantelflächen-Bestimmung bietet der elliptische Kegel ein reichhaltiges Spektrum mathematischer Herausforderungen. Seine praktischen Anwendungen in Optik, Technik und Architektur zeigen, wie mathematische Schönheit und praktischer Nutzen Hand in Hand gehen können. Der elliptische Kegel bleibt ein faszinierendes Beispiel dafür, wie eine scheinbar einfache Variation eines bekannten geometrischen Körpers zu völlig neuen mathematischen Welten führen kann.
|
|
|
|