Doppelkegel Rechner
Rechner und Formeln zur Berechnung eines Doppelkegels
Doppelkegel Rechner
Der Doppelkegel
Der Doppelkegel ist ein Rotationskörper bestehend aus zwei verbundenen Kegeln.
Doppelkegel Eigenschaften
Der symmetrische Rotationskörper: Zwei Kegel an der Basis verbunden
Doppelkegel Struktur
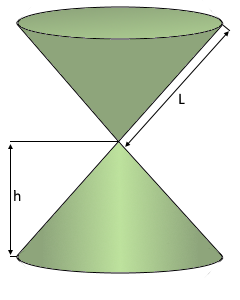
Der Doppelkegel mit perfekter Symmetrie.
Rotationskörper um die Achse.
|
|
Was ist ein Doppelkegel?
Der Doppelkegel ist ein faszinierender Rotationskörper:
- Definition: Zwei Kegel an der Basis verbunden
- Rotationskörper: Durch Rotation einer Doppellinie
- Symmetrie: Perfekte Rotationssymmetrie
- Basisfläche: Gemeinsame kreisförmige Basis
- Mantelflächen: Zwei konische Mantelflächen
- Achse: Zentrale Rotationsachse
Geometrische Eigenschaften des Doppelkegels
Der Doppelkegel zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Radius: r (Radius der Basisfläche)
- Kegelhöhe: h (Höhe eines Kegels)
- Gesamthöhe: 2h (Doppelte Kegelhöhe)
- Mantellänge: L = √(r² + h²)
Besondere Eigenschaften
- Rotationskörper: Symmetrisch um die Achse
- Doppelsymmetrie: Zwei identische Kegel
- Kegelstumpf-verwandt: Spezialfall mit Spitze
- Kontinuierlich: Glatte Mantelflächen
Mathematische Beziehungen
Der Doppelkegel folgt eleganten mathematischen Gesetzen:
Volumen-Formel
Das Volumen ist doppelt so groß wie das eines einzelnen Kegels.
Oberflächen-Formel
Eine Basisfläche plus zwei Mantelflächen.
Anwendungen des Doppelkegels
Doppelkegel finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Dekorative Säulen und Pfeiler
- Turmdächer und Spitzen
- Skulpturale Elemente
- Moderne Architekturformen
Wissenschaft & Technik
- Optische Linsen und Prismen
- Mechanische Kupplungen
- Behälter und Trichter
- Rotationskörper-Studien
Bildung & Lehre
- Geometrie-Unterricht
- Rotationskörper-Studien
- Volumen- und Flächenberechnung
- 3D-Geometrie-Demonstration
Kunst & Design
- Skulpturen und Installationen
- Keramik und Töpferei
- Industriedesign
- Dekorative Objekte
Formeln zum Doppelkegel
Basisfläche (A)
Kreisfläche der gemeinsamen Basis
Mantellänge (L)
Seitenlänge des Kegelmantels (Pythagoras)
Beide Seitenflächen (SL)
Doppelte Mantelfläche beider Kegel
Gesamte Oberfläche (S)
Basis plus beide Mantelflächen
Volumen (V)
Doppeltes Volumen eines einzelnen Kegels
Berechnungsbeispiel für einen Doppelkegel
Gegeben
Gesucht: Alle Eigenschaften des Doppelkegels
1. Mantellänge-Berechnung
Für r = 5, h = 6:
\[L = \sqrt{5^2 + 6^2}\] \[L = \sqrt{25 + 36}\] \[L = \sqrt{61} ≈ 7.81\]Die Mantellänge beträgt etwa 7.81 Längeneinheiten
2. Basisflächen-Berechnung
Für r = 5:
\[A = 5^2 \cdot π\] \[A = 25π\] \[A ≈ 78.54\]Die Basisfläche beträgt etwa 78.54 Flächeneinheiten
3. Seitenflächen-Berechnung
Für r = 5, L ≈ 7.81:
\[S_L = 2 \cdot π \cdot 5 \cdot 7.81\] \[S_L ≈ 2 \cdot π \cdot 39.05\] \[S_L ≈ 245.4\]Die Seitenflächen betragen etwa 245.4 Flächeneinheiten
4. Oberflächen-Berechnung
Für A ≈ 78.54, SL ≈ 245.4:
\[S = 2 \cdot 78.54 + 245.4\] \[S = 157.08 + 245.4\] \[S ≈ 402.5\]Die Oberfläche beträgt etwa 402.5 Flächeneinheiten
5. Volumen-Berechnung
Für r = 5, h = 6:
\[V = \frac{2}{3} \cdot 5^2 \cdot π \cdot 6\] \[V = \frac{2}{3} \cdot 25 \cdot π \cdot 6\] \[V = 100π ≈ 314.2\]Der Doppelkegel mit perfekter Rotationssymmetrie
Der Doppelkegel: Symmetrie in der Rotation
Der Doppelkegel ist ein faszinierender Rotationskörper, der die Eleganz der doppelten Symmetrie verkörpert. Durch die Verbindung zweier identischer Kegel an ihrer gemeinsamen Basis entsteht eine einzigartige Struktur, die sowohl in der Mathematik als auch in praktischen Anwendungen von großer Bedeutung ist. Die mathematische Schönheit liegt in der einfachen Verdopplung der Kegelformeln und der perfekten Rotationssymmetrie um die zentrale Achse, die diesem Körper seine charakteristische Form verleiht.
Die Geometrie der Rotationssymmetrie
Der Doppelkegel zeigt die Perfektion der Rotationssymmetrie:
- Rotationskörper: Entsteht durch Rotation einer Doppellinie um die Achse
- Doppelsymmetrie: Zwei identische Kegel spiegelsymmetrisch verbunden
- Kontinuität: Glatte Übergänge zwischen den Mantelflächen
- Zentrale Achse: Perfekte Rotationssymmetrie um die Hauptachse
- Basisfläche: Gemeinsame kreisförmige Grundfläche beider Kegel
- Mantelflächen: Zwei konische Oberflächen mit identischen Eigenschaften
- Vielseitigkeit: Ideal für technische und künstlerische Anwendungen
Mathematische Eleganz
Einfache Verdopplung
Die Formeln des Doppelkegels folgen dem Prinzip der einfachen Verdopplung der Kegelformeln, was zu eleganten und leicht verständlichen Beziehungen führt.
Pythagoras-Beziehung
Die Mantellänge folgt dem Satz des Pythagoras, was die geometrische Klarheit und mathematische Schönheit des Doppelkegels unterstreicht.
Rotationsprinzip
Als Rotationskörper zeigt der Doppelkegel die fundamentalen Prinzipien der Rotation und ihre Auswirkungen auf Volumen und Oberfläche.
Praktische Anwendbarkeit
Die einfachen Formeln und die symmetrische Struktur machen den Doppelkegel zu einem bevorzugten Objekt in Technik und Design.
Zusammenfassung
Der Doppelkegel verkörpert die perfekte Balance zwischen mathematischer Einfachheit und geometrischer Eleganz. Seine Struktur aus zwei verbundenen Kegeln, beschrieben durch verdoppelte Kegelformeln und die Pythagoras-Beziehung, macht ihn zu einem faszinierenden Studienobjekt für Mathematiker, Ingenieure und Designer. Als Rotationskörper zeigt er, wie die einfache Rotation einer Linie zu komplexen dreidimensionalen Formen führen kann. Von der reinen Geometrie bis zur praktischen Anwendung in Architektur und Technik bleibt der Doppelkegel ein faszinierendes Beispiel für die Kraft der Symmetrie und die Schönheit der mathematischen Transformation. Seine doppelte Struktur symbolisiert Gleichgewicht und Harmonie in der dreidimensionalen Welt.
|
|
|
|