Abgerundeter Kegel Rechner
Rechner und Formeln zur Berechnung eines abgerundeten Kegels
Abgerundeter Kegel Rechner
Der Abgerundete Kegel
Ein abgerundeter Kegel ist eine elegante geometrische Form bestehend aus einem Kegelstumpf mit sphärischer Kappe.
Abgerundeter Kegel Eigenschaften
Die sanfte Form: Kegelstumpf mit sphärischer Abrundung
Kegel Struktur
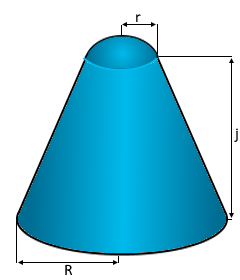
Der abgerundete Kegel mit sphärischer Kappe.
Elegante Verbindung von Kegel und Kugel.
|
|
Was ist ein abgerundeter Kegel?
Ein abgerundeter Kegel ist eine elegante geometrische Form:
- Definition: Kegelstumpf mit sphärischer Kappe
- Komponenten: Konischer Hauptteil und Kugelkappe
- Übergänge: Glatte Verbindung zwischen den Teilen
- Parameter: Basisradius, Kappenradius, Höhe
- Eigenschaften: Aerodynamische Form
- Anwendung: Technik und Architektur
Geometrische Eigenschaften des abgerundeten Kegels
Der abgerundete Kegel zeigt interessante geometrische Eigenschaften:
Grundparameter
- Basisradius: R (größerer Radius)
- Kappenradius: r (kleinerer Radius)
- Kegelstumpfhöhe: j (konischer Teil)
- Kappenhöhe: i (sphärischer Teil)
Besondere Eigenschaften
- Hybrid-Form: Kegel und Kugel kombiniert
- Glatte Übergänge: Kontinuierliche Krümmung
- Aerodynamisch: Optimale Strömungseigenschaften
- Praktisch: Vielseitige Anwendungen
Mathematische Beziehungen
Der abgerundete Kegel folgt komplexen mathematischen Gesetzen:
Volumen-Berechnung
Kombination aus Kegelstumpf- und Kugelkappenvolumen. Komplexe Berechnung.
Oberflächen-Berechnung
Kegelmantel + Basisfläche + Kugelkappe. Trigonometrische Beziehungen.
Anwendungen des abgerundeten Kegels
Abgerundete Kegel finden Anwendung in verschiedenen Bereichen:
Luft- & Raumfahrt
- Raketen-Nasenspitzen
- Flugzeug-Bugkonen
- Triebwerks-Einlässe
- Aerodynamische Komponenten
Industrie & Technik
- Strömungsoptimierte Bauteile
- Ventil- und Düsendesign
- Maschinenbaukomponenten
- Druckbehälter-Abschlüsse
Architektur & Bauwesen
- Moderne Dachkonstruktionen
- Turm- und Schornsteinspitzen
- Dekorative Elemente
- Wassertanks und Silos
Design & Kunst
- Moderne Skulpturen
- Industriedesign-Objekte
- Architektonische Kunst
- Dekorative Formgebung
Formeln zum abgerundeten Kegel
Basiswinkel (α)
Winkel zwischen Kegelachse und Mantellinie
Höhe der Kappe (i)
Höhe der sphärischen Kappe basierend auf dem Winkel
Oberfläche (S)
Mantelfläche + Basisfläche + Kugelfläche
Volumen (V)
Kegelstumpfvolumen + Kugelkappenvolumen
Abgerundeter Kegel Parameter
R (größer)
r (kleiner)
j
i (berechnet)
Alle Eigenschaften folgen aus der geometrischen Verbindung von Kegel und Kugel
Berechnungsbeispiel für einen abgerundeten Kegel
Gegeben
Gesucht: Alle Eigenschaften des abgerundeten Kegels
1. Basiswinkel-Berechnung
Für R=4, r=3, j=4:
\[α = \arccos\left( \frac{4 - 3}{\sqrt{ 4^2 + ( 4 - 3 )^2}} \right)\] \[α = \arccos\left( \frac{1}{\sqrt{17}} \right)\] \[α ≈ 75.96°\]Der Basiswinkel beträgt etwa 75.96°
2. Kappenhöhen-Berechnung
Mit α ≈ 75.96°:
\[i = \sqrt{\frac{ 3^2 }{\frac{ 2 }{ 1 - \cos(75.96°) } - 1 }}\] \[i ≈ 1.86\]Die Kappenhöhe beträgt etwa 1.86 Einheiten
3. Oberflächen-Berechnung
Mantelfläche + Basis + Kappe:
\[S = (4 + 3) \cdot π \cdot \sqrt{1^2 + 4^2} + π \cdot 4^2 + π \cdot (3^2 + 1.86^2)\] \[S ≈ 141.37\]Die Oberfläche beträgt etwa 141.37 Flächeneinheiten
4. Der perfekte abgerundete Kegel
Der abgerundete Kegel mit eleganter sphärischer Kappe
Der abgerundete Kegel: Elegante Verbindung von Geometrie und Glätte
Der abgerundete Kegel ist eine faszinierende geometrische Form, die die klassische Eleganz des Kegels mit der sanften Vollendung einer Kugel verbindet. Diese einzigartige Kombination aus einem konischen Hauptteil und einer sphärischen Kappe schafft eine harmonische Struktur, die sowohl mathematisch anspruchsvoll als auch ästhetisch ansprechend ist. Die mathematische Schönheit liegt in den komplexen Beziehungen zwischen trigonometrischen Funktionen, Kegelgeometrie und Kugelgeometrie, die alle Parameter in perfekter Harmonie miteinander verknüpfen.
Die Geometrie der sanften Übergänge
Der abgerundete Kegel zeigt die Perfektion der kombinierten Geometrie:
- Hybrid-Struktur: Nahtlose Verbindung von Kegel und Kugel
- Kontinuierliche Krümmung: Glatte Übergänge ohne Kanten
- Aerodynamische Form: Optimierte Strömungseigenschaften
- Parameterabhängigkeit: Drei Hauptparameter bestimmen die Form
- Trigonometrische Beziehungen: Winkel bestimmen die Proportionen
- Praktische Eleganz: Funktional und ästhetisch ansprechend
- Vielseitigkeit: Breite Anwendungsmöglichkeiten
Mathematische Komplexität in eleganter Form
Trigonometrische Eleganz
Die Berechnung des abgerundeten Kegels nutzt inverse trigonometrische Funktionen und komplexe Flächenintegrale, die die Verbindung zwischen Kegel und Kugel beschreiben.
Geometrische Harmonie
Die Parameter R, r und j bestimmen nicht nur die Größe, sondern auch die Proportionen und damit die ästhetische Wirkung der gesamten Form.
Strömungsoptimierung
Die abgerundete Form minimiert Turbulenzen und optimiert Strömungseigenschaften, was sie ideal für technische Anwendungen macht.
Praktische Perfektion
Die Kombination aus struktureller Stabilität und aerodynamischer Effizienz macht diese Form zu einer bevorzugten Wahl in Technik und Design.
Zusammenfassung
Der abgerundete Kegel verkörpert die elegante Vereinigung zweier fundamentaler geometrischer Formen zu einer harmonischen Einheit. Seine Struktur aus einem konischen Hauptteil und einer sphärischen Kappe, beschrieben durch komplexe trigonometrische und geometrische Beziehungen, macht ihn zu einem faszinierenden Studienobjekt für Mathematiker, Ingenieure und Designer. Von der Luft- und Raumfahrt bis zur modernen Architektur zeigt der abgerundete Kegel, wie mathematische Eleganz und praktische Funktionalität in perfekter Harmonie vereint werden können. Seine glatten Übergänge und optimierten Strömungseigenschaften machen ihn zu einer zeitlosen Form, die sowohl technische Anforderungen erfüllt als auch ästhetische Vollendung verkörpert.
|
|
|
|