Cylindrical Segment Calculator
Calculator and formulas for calculating a cylindrical segment
Cylindrical Segment Calculator
The Cylindrical Segment
The cylindrical segment is a cut-off cylinder piece with a characteristic segment shape.
Cylindrical Segment Properties
The Cylindrical Segment: Cut-off cylinder piece with circular segment cross-section
Cylindrical Segment Visualization
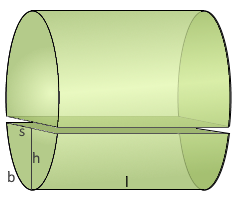
Cylindrical Segment
Cut-off cylinder piece
Parameters
r: Radius of the cylinder
h: Segment height (cap height)
l: Length of the segment
s: Segment width (chord)
b: Arc length of the segment
Segment of a cylinder.
Circular segment as cross-section.
|
|
What is a Cylindrical Segment?
The cylindrical segment is an important geometric body:
- Definition: Cut-off piece of a circular cylinder
- Cross-section: Circular segment as characteristic cutting surface
- Properties: Segment width s and arc length b as important parameters
- Cap height h: Determines the size of the cut-off area
- Applications: Container construction, piping technology, architecture
- Mathematics: Combination of circular segment and cylinder geometry
Geometric Properties of the Cylindrical Segment
The cylindrical segment shows characteristic geometric properties:
Basic Parameters
- Radius r: Radius of the original cylinder
- Segment height h: Height of the cut-off cap
- Segment length l: Length of the cylindrical segment
- Segment width s: Chord of the circular segment
Special Properties
- Circular segment cross-section: Characteristic cutting surface
- Arc length b: Circular arc of the segment
- Cap shape: Curved segment surface
- Chord relationship: s = 2√(2rh - h²)
Mathematical Relationships of the Cylindrical Segment
The cylindrical segment follows elegant mathematical laws:
Segment Width Formula
Chord of the circular segment through elegant square root formula.
Arc Length Formula
Arc length through inverse trigonometric function.
Applications of the Cylindrical Segment
Cylindrical segments find applications in various fields:
Container & Tank Construction
- Partially filled cylinder tanks
- Pressure vessel segments
- Silos and storage tanks
- Pipeline sections
Architecture & Construction
- Vault constructions
- Tunnel segments
- Bridge arches
- Roof constructions
Process Engineering
- Reactor vessel segments
- Mixing vessel sections
- Distillation columns
- Heat exchanger elements
Water Engineering & Hydraulics
- Channel cross-sections
- Pipeline segments
- Culvert constructions
- Sewage lines
Formulas for the Cylindrical Segment
Segment Width (s)
Chord of the circular segment
Arc Length (b)
Circular arc length of the segment
End Area (AT)
Segment area at the ends
Volume (V)
Segment area times length
Additional Formulas
\[L = l \cdot b\]
\[A = s \cdot l\]
\[S = L + A + 2A_T\]
\[\alpha = 2\arccos\left(\frac{r-h}{r}\right)\]
The cylindrical segment connects circular segment and cylinder geometry
Calculation Example for a Cylindrical Segment
Given
Find: All parameters of the cylindrical segment
1. Calculate Segment Width
For r = 5 cm, h = 3 cm:
\[s = 2\sqrt{2rh - h^2}\] \[s = 2\sqrt{2 \cdot 5 \cdot 3 - 3^2}\] \[s = 2\sqrt{30 - 9} = 2\sqrt{21}\] \[s ≈ 2 \cdot 4.583 ≈ 9.17 \text{ cm}\]The segment width is approximately 9.17 cm
2. Calculate Arc Length
Arc length of the circular segment:
\[b = r \cdot 2 \cdot \arccos\left(\frac{r-h}{r}\right)\] \[b = 5 \cdot 2 \cdot \arccos\left(\frac{5-3}{5}\right)\] \[b = 10 \cdot \arccos(0.4)\] \[b ≈ 10 \cdot 1.159 ≈ 11.59 \text{ cm}\]The arc length is approximately 11.59 cm
3. Calculate End Area
Segment area at the ends:
\[A_T = \frac{rb}{2} - \frac{s(r-h)}{2}\] \[A_T = \frac{5 \cdot 11.59}{2} - \frac{9.17 \cdot (5-3)}{2}\] \[A_T = \frac{57.95}{2} - \frac{9.17 \cdot 2}{2}\] \[A_T ≈ 28.98 - 9.17 ≈ 19.81 \text{ cm}^2\]The end area is approximately 19.81 cm²
4. Calculate Volume
Volume of the cylindrical segment:
\[V = A_T \cdot l\] \[V = 19.81 \cdot 9\] \[V ≈ 178.29 \text{ cm}^3\]The volume is approximately 178.29 cm³
5. Additional Calculations
\[L = l \cdot b = 9 \cdot 11.59 ≈ 104.31 \text{ cm}^2\]
\[A = s \cdot l = 9.17 \cdot 9 ≈ 82.53 \text{ cm}^2\]
\[S = L + A + 2A_T ≈ 226.46 \text{ cm}^2\]
All surface components of the cylindrical segment
6. Geometric Analysis
α = 2·arccos(0.4) ≈ 131.8°
131.8°/360° ≈ 36.6% of full circle
h/r = 3/5 = 0.6 (60%)
The segment comprises about 36.6% of the full circle at 60% of radius height
7. Summary
The cylindrical segment with all characteristic parameters
8. Practical Example: Partially Filled Tank
V ≈ 178.29 cm³
≈ 0.18 liters
Lateral area L ≈ 104.31 cm²
Contact area
60% of radius height
36.6% of cross-section
A horizontal cylindrical tank with 60% fill height for precise volume determination
9. Comparison with Full Cylinder
r=5, h=3, l=9
V≈178.29 cm³
r=5, l=9
V≈706.86 cm³
178.29/706.86 ≈ 25.2%
Segment fraction
The segment contains about 25.2% of the full cylinder volume - precise partial filling!
The Cylindrical Segment: Precision of Segment Geometry
The cylindrical segment is a fascinating geometric body that combines the elegance of circular segment geometry with the practicality of cylindrical forms. As a cut-off piece of a circular cylinder, it unites the mathematical complexity of segment calculation with technical applicability in container construction, piping technology, and architecture. This unique combination of segment-shaped beauty and functional versatility makes it an indispensable element in modern engineering.
The Geometry of Segment Form
The cylindrical segment shows the perfection of segmental geometry:
- Circular segment cross-section: Characteristic cutting surface with segment width s
- Segment width s = 2√(2rh-h²): Elegant square root formula for the chord
- Arc length b = r·2·arccos((r-h)/r): Inverse trigonometric relationship
- Cap height h: Determines the size of the cut-off area
- Segment area AT: Combination of circular sector and triangle area
- Central angle α: Characteristic central angle of the segment
- Volume principle V = AT·l: Segment area times length gives the volume
Versatile Applications
Container Construction Precision
Partially filled cylinder tanks and pressure vessels use segment calculations for precise volume determination and optimal fill level monitoring.
Architectural Elegance
Vault constructions and tunnel segments use segment geometry for structurally stable and aesthetically pleasing structures with characteristic form.
Process Engineering Efficiency
Reactor vessels and mixing vessel sections use segment forms for optimized flow guidance and uniform process distribution.
Hydraulic Innovation
Channel cross-sections and pipeline segments use segment geometry for flow-optimized water guidance with minimal friction losses.
Summary
The cylindrical segment embodies the perfect synthesis of segment-geometric precision and practical functionality. Its form, characterized by the cap height h and described by the elegant formulas for segment width s = 2√(2rh-h²) and arc length b = r·2·arccos((r-h)/r), shows the mathematical sophistication of circular segment geometry. The segment area AT as a combination of circular sector and basic geometric forms demonstrates how complex area calculations are transformed into practical volume determination V = AT·l. From precise tank fillings to elegant vault constructions to flow-optimized channel profiles - the cylindrical segment proves that the most beautiful geometric forms often also offer the most functional solutions. It is living proof that segment geometry possesses not only mathematical elegance but also finds concrete applications in modern technology, showing how circular segments and cylinder form merge in perfect harmony.