Zylinder-Segment Rechner
Rechner und Formeln zur Berechnung eines Zylinder-Segments
Zylinder-Segment Rechner
Das Zylinder-Segment
Das Zylinder-Segment ist ein abgeschnittenes Zylinderstück mit charakteristischer Segmentform.
Zylinder-Segment Eigenschaften
Das Zylinder-Segment: Abgeschnittenes Zylinderstück mit Kreissegment-Querschnitt
Zylinder-Segment Visualisierung
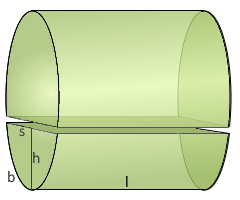
Zylinder-Segment
Abgeschnittenes Zylinderstück
Parameter
r: Radius des Zylinders
h: Segmenthöhe (Kalottenhöhe)
l: Länge des Segments
s: Segmentbreite (Sehne)
b: Bogenlänge des Segments
Segment eines Zylinders.
Kreissegment als Querschnitt.
|
|
Was ist ein Zylinder-Segment?
Das Zylinder-Segment ist ein wichtiger geometrischer Körper:
- Definition: Abgeschnittenes Stück eines Kreiszylinders
- Querschnitt: Kreissegment als charakteristische Schnittfläche
- Eigenschaften: Segmentbreite s und Bogenlänge b als wichtige Parameter
- Kalottenhöhe h: Bestimmt die Größe des abgeschnittenen Bereichs
- Anwendung: Behälterbau, Rohrleitungstechnik, Architektur
- Mathematik: Kombination aus Kreissegment- und Zylindergeometrie
Geometrische Eigenschaften des Zylinder-Segments
Das Zylinder-Segment zeigt charakteristische geometrische Eigenschaften:
Grundparameter
- Radius r: Radius des ursprünglichen Zylinders
- Segmenthöhe h: Höhe der abgeschnittenen Kalotte
- Segmentlänge l: Länge des Zylinder-Segments
- Segmentbreite s: Sehne des Kreissegments
Besondere Eigenschaften
- Kreissegment-Querschnitt: Charakteristische Schnittfläche
- Bogenlänge b: Kreisbogen des Segments
- Kalottenform: Gewölbte Segmentoberfläche
- Sehnenbeziehung: s = 2√(2rh - h²)
Mathematische Beziehungen des Zylinder-Segments
Das Zylinder-Segment folgt eleganten mathematischen Gesetzen:
Segmentbreite-Formel
Sehne des Kreissegments durch elegante Wurzelformel.
Bogenlängen-Formel
Bogenlänge durch inverse trigonometrische Funktion.
Anwendungen des Zylinder-Segments
Zylinder-Segmente finden Anwendung in verschiedenen Bereichen:
Behälterbau & Tankbau
- Teilweise gefüllte Zylindertanks
- Druckbehälter-Segmente
- Silos und Lagertanks
- Rohrleitungs-Abschnitte
Architektur & Bauwesen
- Gewölbekonstruktionen
- Tunnelsegmente
- Brückenbogen
- Dachkonstruktionen
Verfahrenstechnik
- Reaktorbehälter-Segmente
- Mischbehälter-Abschnitte
- Destillationskolonnen
- Wärmetauscher-Elemente
Wasserbau & Hydraulik
- Kanalquerschnitte
- Rohrleitungs-Segmente
- Durchlass-Konstruktionen
- Abwasserleitungen
Formeln zum Zylinder-Segment
Segmentbreite (s)
Sehne des Kreissegments
Bogenlänge (b)
Kreisbogenlänge des Segments
Seitenfläche (AT)
Segmentfläche an den Enden
Volumen (V)
Segmentfläche mal Länge
Weitere Formeln
\[L = l \cdot b\]
\[A = s \cdot l\]
\[S = L + A + 2A_T\]
\[\alpha = 2\arccos\left(\frac{r-h}{r}\right)\]
Das Zylinder-Segment verbindet Kreissegment- und Zylindergeometrie
Berechnungsbeispiel für ein Zylinder-Segment
Gegeben
Gesucht: Alle Parameter des Zylinder-Segments
1. Segmentbreite berechnen
Für r = 5 cm, h = 3 cm:
\[s = 2\sqrt{2rh - h^2}\] \[s = 2\sqrt{2 \cdot 5 \cdot 3 - 3^2}\] \[s = 2\sqrt{30 - 9} = 2\sqrt{21}\] \[s ≈ 2 \cdot 4.583 ≈ 9.17 \text{ cm}\]Die Segmentbreite beträgt etwa 9.17 cm
2. Bogenlänge berechnen
Bogenlänge des Kreissegments:
\[b = r \cdot 2 \cdot \arccos\left(\frac{r-h}{r}\right)\] \[b = 5 \cdot 2 \cdot \arccos\left(\frac{5-3}{5}\right)\] \[b = 10 \cdot \arccos(0.4)\] \[b ≈ 10 \cdot 1.159 ≈ 11.59 \text{ cm}\]Die Bogenlänge beträgt etwa 11.59 cm
3. Seitenfläche berechnen
Segmentfläche an den Enden:
\[A_T = \frac{rb}{2} - \frac{s(r-h)}{2}\] \[A_T = \frac{5 \cdot 11.59}{2} - \frac{9.17 \cdot (5-3)}{2}\] \[A_T = \frac{57.95}{2} - \frac{9.17 \cdot 2}{2}\] \[A_T ≈ 28.98 - 9.17 ≈ 19.81 \text{ cm}^2\]Die Seitenfläche beträgt etwa 19.81 cm²
4. Volumen berechnen
Volumen des Zylinder-Segments:
\[V = A_T \cdot l\] \[V = 19.81 \cdot 9\] \[V ≈ 178.29 \text{ cm}^3\]Das Volumen beträgt etwa 178.29 cm³
5. Weitere Berechnungen
\[L = l \cdot b = 9 \cdot 11.59 ≈ 104.31 \text{ cm}^2\]
\[A = s \cdot l = 9.17 \cdot 9 ≈ 82.53 \text{ cm}^2\]
\[S = L + A + 2A_T ≈ 226.46 \text{ cm}^2\]
Alle Oberflächenkomponenten des Zylinder-Segments
6. Geometrische Analyse
α = 2·arccos(0.4) ≈ 131.8°
131.8°/360° ≈ 36.6% des Vollkreises
h/r = 3/5 = 0.6 (60%)
Das Segment umfasst etwa 36.6% des Vollkreises bei 60% der Radiushöhe
7. Zusammenfassung
Das Zylinder-Segment mit allen charakteristischen Parametern
8. Praktisches Beispiel: Teilweise gefüllter Tank
V ≈ 178.29 cm³
≈ 0.18 Liter
Mantelfläche L ≈ 104.31 cm²
Kontaktfläche
60% der Radiushöhe
36.6% des Querschnitts
Ein liegender Zylindertank mit 60% Füllhöhe für präzise Volumenbestimmung
9. Vergleich mit Vollzylinder
r=5, h=3, l=9
V≈178.29 cm³
r=5, l=9
V≈706.86 cm³
178.29/706.86 ≈ 25.2%
Segment-Anteil
Das Segment enthält etwa 25.2% des Vollzylinder-Volumens - präzise Teilfüllung!
Das Zylinder-Segment: Präzision der Segmentgeometrie
Das Zylinder-Segment ist ein faszinierender geometrischer Körper, der die Eleganz der Kreissegmentgeometrie mit der Praktikabilität zylindrischer Formen verbindet. Als abgeschnittenes Stück eines Kreiszylinders vereint es in sich die mathematische Komplexität der Segmentberechnung mit der technischen Anwendbarkeit in Behälterbau, Rohrleitungstechnik und Architektur. Diese einzigartige Kombination aus segmentförmiger Schönheit und funktionaler Vielseitigkeit macht es zu einem unverzichtbaren Element in der modernen Ingenieurstechnik.
Die Geometrie der Segmentform
Das Zylinder-Segment zeigt die Perfektion segmentaler Geometrie:
- Kreissegment-Querschnitt: Charakteristische Schnittfläche mit Segmentbreite s
- Segmentbreite s = 2√(2rh-h²): Elegante Wurzelformel für die Sehne
- Bogenlänge b = r·2·arccos((r-h)/r): Inverse trigonometrische Beziehung
- Kalottenhöhe h: Bestimmt die Größe des abgeschnittenen Bereichs
- Segmentfläche AT: Kombination aus Kreissektor und Dreiecksfläche
- Mittelpunktswinkel α: Charakteristischer Zentralwinkel des Segments
- Volumenprinzip V = AT·l: Segmentfläche mal Länge ergibt das Volumen
Vielseitige Anwendungen
Behälterbau-Präzision
Teilweise gefüllte Zylindertanks und Druckbehälter nutzen Segment-Berechnungen für präzise Volumenbestimmung und optimale Füllstandsüberwachung.
Architektonische Eleganz
Gewölbekonstruktionen und Tunnelsegmente verwenden die Segmentgeometrie für strukturell stabile und ästhetisch ansprechende Bauwerke mit charakteristischer Form.
Verfahrenstechnische Effizienz
Reaktorbehälter und Mischbehälter-Abschnitte nutzen Segmentformen für optimierte Strömungsführung und gleichmäßige Prozessverteilung.
Hydraulische Innovation
Kanalquerschnitte und Rohrleitungs-Segmente verwenden die Segmentgeometrie für strömungsoptimierte Wasserführung mit minimalen Reibungsverlusten.
Zusammenfassung
Das Zylinder-Segment verkörpert die perfekte Synthese aus segmentgeometrischer Präzision und praktischer Funktionalität. Seine durch die Kalottenhöhe h charakterisierte Form, beschrieben durch die eleganten Formeln für Segmentbreite s = 2√(2rh-h²) und Bogenlänge b = r·2·arccos((r-h)/r), zeigt die mathematische Raffinesse der Kreissegmentgeometrie. Die Segmentfläche AT als Kombination aus Kreissektor und geometrischen Grundformen demonstriert, wie komplexe Flächenberechnungen in praktische Volumenbestimmung V = AT·l überführt werden. Von präzisen Tankfüllungen über elegante Gewölbekonstruktionen bis hin zu strömungsoptimierten Kanalprofilen - das Zylinder-Segment beweist, dass die schönsten geometrischen Formen oft auch die funktionalsten Lösungen bieten. Es ist der lebende Beweis dafür, dass Segmentgeometrie nicht nur mathematische Eleganz besitzt, sondern auch konkrete Anwendungen in der modernen Technik findet und zeigt, wie Kreissegmente und Zylinderform in perfekter Harmonie verschmelzen.
|
|
|
|