Cylindrical Wedge Calculator
Calculator and formulas for calculating a cylindrical wedge
Cylindrical Wedge Calculator
The Cylindrical Wedge
The cylindrical wedge is a sector-shaped cylinder section with a defined central angle φ.
Cylindrical Wedge Properties
The Cylindrical Wedge: Sector-shaped section from a circular cylinder
Cylindrical Wedge Visualization
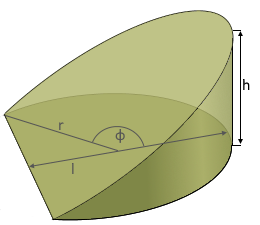
Cylindrical Wedge
Sector-shaped cylinder section
Parameters
r: Radius of the cylinder
h: Height of the cylindrical wedge
φ: Central angle (0° - 180°)
l: Wedge length (chord)
Sector-shaped cylinder section.
Defined by central angle φ.
What is a Cylindrical Wedge?
The cylindrical wedge is a fascinating geometric body:
- Definition: Sector-shaped section from a circular cylinder
- Central angle φ: Determines the size of the wedge section (0° - 180°)
- Properties: Radially symmetric form with wedge-shaped cross-section
- Wedge length l: Chord of the circular section (dependent on angle)
- Applications: Mechanical engineering, architecture, piping technology
- Mathematics: Combination of sector and cylinder geometry
Geometric Properties of the Cylindrical Wedge
The cylindrical wedge shows characteristic geometric properties:
Basic Parameters
- Radius r: Radius of the circular base
- Height h: Height of the cylindrical wedge
- Central angle φ: Angle of the sector section
- Wedge length l: Chord of the circular sector
Special Properties
- Radial symmetry: Symmetry around the cylinder axis
- Sector-shaped cross-section: Circular section as base
- Angle-dependent wedge length: l = f(r, φ) depending on angle size
- Wedge-shaped lateral surface: Curved trapezoidal surface
Mathematical Relationships of the Cylindrical Wedge
The cylindrical wedge follows complex mathematical laws:
Volume Formula
Complex formula with trigonometric functions. Elegant sector geometry.
Wedge Length Formula
Chord of the circular sector, dependent on angle φ. ± depending on φ ≥ 90° or φ < 90°.
Applications of the Cylindrical Wedge
Cylindrical wedges find applications in various fields:
Mechanical Engineering & Automotive
- V-belts and V-belt pulleys
- Gear sector elements
- Crankshaft segments
- Valve control components
Architecture & Construction
- Arch constructions
- Vault elements
- Stair railings
- Column segments
Piping Technology
- Pipe bend segments
- Flange components
- Valve housing parts
- Branch elements
Science & Technology
- Optical components
- Measuring device sectors
- Turbine blades
- Drive elements
Formulas for the Cylindrical Wedge
Wedge Length (l) - φ ≥ 90°
For angles greater than or equal to 90°
Wedge Length (l) - φ < 90°
For angles less than 90°
Volume (V)
Complex volume formula with trigonometric functions
Lateral Area (L)
Curved lateral surface of the cylindrical wedge
Additional Parameters
\[\phi \text{ (in degrees)}\]
\[A = \frac{\phi}{360°} \cdot \pi r^2\]
\[s = \frac{\phi}{180°} \cdot \pi r\]
\[\phi_{rad} = \frac{\phi \cdot \pi}{180°}\]
The cylindrical wedge perfectly connects sector and cylinder geometry
Calculation Example for a Cylindrical Wedge
Given
Find: All parameters of the cylindrical wedge
1. Wedge Length Calculation
For φ = 90° ≥ 90°, use first formula:
\[l = r + \sqrt{r^2 - r^2 \sin^2(\phi)}\] \[\sin(90°) = 1\] \[l = 5 + \sqrt{25 - 25 \cdot 1^2}\] \[l = 5 + \sqrt{0} = 5.0 \text{ cm}\]The wedge length is exactly 5.0 cm (= radius)
2. Trigonometric Values
For φ = 90°:
\[\sin(90°) = 1\] \[\cos(90°) = 0\] \[\sin^3(90°) = 1^3 = 1\] \[90° = \frac{\pi}{2} \text{ rad}\]Special case: φ = 90° gives simple values
3. Volume Calculation
Complex volume formula simplified:
\[V = hr^2 \frac{3\sin(90°) - 3 \cdot 90° \cdot \cos(90°) - \sin^3(90°)}{3(1-\cos(90°))}\] \[V = 6 \cdot 25 \frac{3 \cdot 1 - 3 \cdot \frac{\pi}{2} \cdot 0 - 1}{3(1-0)}\] \[V = 150 \frac{3 - 0 - 1}{3} = 150 \cdot \frac{2}{3} = 100 \text{ cm}^3\]The volume is exactly 100 cm³
4. Lateral Area Calculation
Lateral area formula for φ = 90°:
\[L = \frac{2hr(\sin(90°) - 90° \cdot \cos(90°))}{1 - \cos(90°)}\] \[L = \frac{2 \cdot 6 \cdot 5 \cdot (1 - \frac{\pi}{2} \cdot 0)}{1 - 0}\] \[L = \frac{60 \cdot 1}{1} = 60 \text{ cm}^2\]The lateral area is 60 cm²
5. Geometric Analysis
90°/360° = 1/4 = 25% of full cylinder
V_full = πr²h = π·25·6 ≈ 471.24 cm³
100/471.24 ≈ 21.2% (< 25% due to wedge effect)
The wedge effect reduces volume compared to a simple sector
6. Summary
The cylindrical wedge with 90° central angle - a quarter sector with wedge characteristics
7. Practical Example: V-Belt Pulley
V = 100 cm³
≈ 0.1 liters
L = 60 cm²
Coating area
90° wedge angle
Optimal power transmission
A V-belt pulley with 90° sector for optimal power transmission
8. Special Case φ = 90°
φ = 90° is a boundary case
Wedge length l = radius r
Perfect quarter symmetry
sin(90°) = 1, cos(90°) = 0
Standard wedge angle
Frequently used
The 90° cylindrical wedge is a mathematically elegant and practically important special case
The Cylindrical Wedge: Sectorial Precision in Geometry
The cylindrical wedge is a fascinating geometric body that combines the elegance of circular sector geometry with the practicality of cylindrical forms. As a sector-shaped section from a circular cylinder, it unites the mathematical complexity of trigonometric functions with technical applicability in mechanical engineering and architecture. This unique combination of radially symmetric beauty and functional versatility makes it an indispensable element in modern construction technology.
The Geometry of the Wedge Sector
The cylindrical wedge shows the perfection of sectorial geometry:
- Central angle φ: Determines the size of the sector section (0° - 180°)
- Angle-dependent wedge length: l = r ± √(r² - r²sin²(φ)) depending on angle size
- Complex volume formula: Trigonometric functions in elegant combination
- Radial symmetry: Perfect symmetry around the cylinder axis
- Sector-shaped cross-section: Circular section as characteristic base
- Wedge effect: Volume smaller than simple circular sector
- Lateral surface curvature: Curved trapezoidal surface geometry
Technical Applications
Mechanical Engineering Precision
V-belt pulleys and gear sectors use precise wedge geometry for optimal power transmission and minimal friction losses in drive systems.
Architectural Elegance
Arch constructions and vault elements use cylindrical wedges for structurally stable and aesthetically pleasing structures with characteristic sector form.
Piping Innovation
Pipe bend segments and flange components use wedge geometry for flow-optimized connections with minimal pressure losses.
Scientific Precision
Optical components and measuring device sectors use cylindrical wedges for precise angle determination and light guidance in scientific instruments.
Summary
The cylindrical wedge embodies the perfect synthesis of trigonometric complexity and practical functionality. Its form, characterized by the central angle φ and described by the elegant formulas for wedge length l = r ± √(r² - r²sin²(φ)) and the complex volume V = hr²[3sin(φ)-3φcos(φ)-sin³(φ)]/[3(1-cos(φ))], shows the mathematical sophistication of sectorial geometry. The angle-dependent wedge length and the characteristic wedge effect demonstrate how trigonometric functions enable practical construction solutions. From precise V-belt pulleys to elegant arch constructions to flow-optimized piping components - the cylindrical wedge proves that the most complex mathematical relationships often lead to the most beautiful and functional technical solutions. It is living proof that sectorial geometry possesses not only mathematical elegance but also finds concrete applications in modern technology, showing how angular geometry and cylinder form merge in perfect harmony.