Zylinderkeil Rechner
Rechner und Formeln zur Berechnung eines Zylinderkeils
Zylinderkeil Rechner
Der Zylinderkeil
Der Zylinderkeil ist ein sektorförmiger Zylinderabschnitt mit definiertem Zentralwinkel φ.
Zylinderkeil Eigenschaften
Der Zylinderkeil: Sektorförmiger Ausschnitt aus einem Kreiszylinder
Zylinderkeil Visualisierung
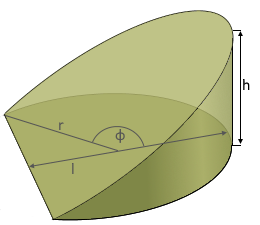
Zylinderkeil
Sektorförmiger Zylinderabschnitt
Parameter
r: Radius des Zylinders
h: Höhe des Zylinderkeils
φ: Zentralwinkel (0° - 180°)
l: Keillänge (Sehne)
Sektorförmiger Zylinderabschnitt.
Definiert durch Zentralwinkel φ.
|
|
Was ist ein Zylinderkeil?
Der Zylinderkeil ist ein faszinierender geometrischer Körper:
- Definition: Sektorförmiger Ausschnitt aus einem Kreiszylinder
- Zentralwinkel φ: Bestimmt die Größe des Keilabschnitts (0° - 180°)
- Eigenschaften: Radialsymmetrische Form mit keilförmigem Querschnitt
- Keillänge l: Sehne des Kreisausschnitts (abhängig vom Winkel)
- Anwendung: Maschinenbau, Architektur, Rohrleitungstechnik
- Mathematik: Kombination aus Sektor- und Zylindergeometrie
Geometrische Eigenschaften des Zylinderkeils
Der Zylinderkeil zeigt charakteristische geometrische Eigenschaften:
Grundparameter
- Radius r: Radius der kreisförmigen Grundfläche
- Höhe h: Höhe des Zylinderkeils
- Zentralwinkel φ: Winkel des Sektorausschnitts
- Keillänge l: Sehne des Kreissektors
Besondere Eigenschaften
- Radialsymmetrie: Symmetrie um die Zylinderachse
- Sektorförmiger Querschnitt: Kreisausschnitt als Grundfläche
- Winkelabhängige Keillänge: l = f(r, φ) je nach Winkelgröße
- Keilförmige Mantelfläche: Gekrümmte trapezoidale Oberfläche
Mathematische Beziehungen des Zylinderkeils
Der Zylinderkeil folgt komplexen mathematischen Gesetzen:
Volumen-Formel
Komplexe Formel mit trigonometrischen Funktionen. Elegante Sektorgeometrie.
Keillängen-Formel
Sehne des Kreissektors, abhängig vom Winkel φ. ± je nach φ ≥ 90° oder φ < 90°.
Anwendungen des Zylinderkeils
Zylinderkeile finden Anwendung in verschiedenen Bereichen:
Maschinenbau & Automotive
- Keilriemen und Keilriemenscheiben
- Zahnradsektor-Elemente
- Kurbelwellen-Segmente
- Ventilsteuerung-Komponenten
Architektur & Bauwesen
- Bogenkonstruktionen
- Gewölbe-Elemente
- Treppengeländer
- Säulen-Segmente
Rohrleitungstechnik
- Rohrbogen-Segmente
- Flansch-Komponenten
- Ventil-Gehäuseteile
- Abzweig-Elemente
Wissenschaft & Technik
- Optische Komponenten
- Messgeräte-Sektoren
- Turbinen-Schaufeln
- Antriebselemente
Formeln zum Zylinderkeil
Keillänge (l) - φ ≥ 90°
Für Winkel größer oder gleich 90°
Keillänge (l) - φ < 90°
Für Winkel kleiner als 90°
Volumen (V)
Komplexe Volumenformel mit trigonometrischen Funktionen
Mantelfläche (L)
Gekrümmte Mantelfläche des Zylinderkeils
Weitere Parameter
\[\phi \text{ (in Grad)}\]
\[A = \frac{\phi}{360°} \cdot \pi r^2\]
\[s = \frac{\phi}{180°} \cdot \pi r\]
\[\phi_{rad} = \frac{\phi \cdot \pi}{180°}\]
Der Zylinderkeil verbindet Sektor- und Zylindergeometrie perfekt
Berechnungsbeispiel für einen Zylinderkeil
Gegeben
Gesucht: Alle Parameter des Zylinderkeils
1. Keillängen-Berechnung
Für φ = 90° ≥ 90°, verwende erste Formel:
\[l = r + \sqrt{r^2 - r^2 \sin^2(\phi)}\] \[\sin(90°) = 1\] \[l = 5 + \sqrt{25 - 25 \cdot 1^2}\] \[l = 5 + \sqrt{0} = 5.0 \text{ cm}\]Die Keillänge beträgt genau 5.0 cm (= Radius)
2. Trigonometrische Werte
Für φ = 90°:
\[\sin(90°) = 1\] \[\cos(90°) = 0\] \[\sin^3(90°) = 1^3 = 1\] \[90° = \frac{\pi}{2} \text{ rad}\]Spezialfall: φ = 90° ergibt einfache Werte
3. Volumen-Berechnung
Komplexe Volumenformel vereinfacht:
\[V = hr^2 \frac{3\sin(90°) - 3 \cdot 90° \cdot \cos(90°) - \sin^3(90°)}{3(1-\cos(90°))}\] \[V = 6 \cdot 25 \frac{3 \cdot 1 - 3 \cdot \frac{\pi}{2} \cdot 0 - 1}{3(1-0)}\] \[V = 150 \frac{3 - 0 - 1}{3} = 150 \cdot \frac{2}{3} = 100 \text{ cm}^3\]Das Volumen beträgt genau 100 cm³
4. Mantelflächen-Berechnung
Mantelflächenformel für φ = 90°:
\[L = \frac{2hr(\sin(90°) - 90° \cdot \cos(90°))}{1 - \cos(90°)}\] \[L = \frac{2 \cdot 6 \cdot 5 \cdot (1 - \frac{\pi}{2} \cdot 0)}{1 - 0}\] \[L = \frac{60 \cdot 1}{1} = 60 \text{ cm}^2\]Die Mantelfläche beträgt 60 cm²
5. Geometrische Analyse
90°/360° = 1/4 = 25% des Vollzylinders
V_voll = πr²h = π·25·6 ≈ 471.24 cm³
100/471.24 ≈ 21.2% (< 25% wegen Keilform)
Der Keileffekt reduziert das Volumen gegenüber einem einfachen Sektor
6. Zusammenfassung
Der Zylinderkeil mit 90° Zentralwinkel - ein Viertel-Sektor mit Keilcharakteristik
7. Praktisches Beispiel: Keilriemenscheibe
V = 100 cm³
≈ 0.1 Liter
L = 60 cm²
Beschichtungsfläche
90° Keilwinkel
Optimale Kraftübertragung
Eine Keilriemenscheibe mit 90° Sektor für optimale Kraftübertragung
8. Spezialfall φ = 90°
φ = 90° ist ein Grenzfall
Keillänge l = Radius r
Perfekte Viertel-Symmetrie
sin(90°) = 1, cos(90°) = 0
Standard-Keilwinkel
Häufig verwendet
Der 90°-Zylinderkeil ist ein mathematisch eleganter und praktisch wichtiger Spezialfall
Der Zylinderkeil: Sektoriale Präzision in der Geometrie
Der Zylinderkeil ist ein faszinierender geometrischer Körper, der die Eleganz der Kreissektorgeometrie mit der Praktikabilität zylindrischer Formen verbindet. Als sektorförmiger Ausschnitt aus einem Kreiszylinder vereint er in sich die mathematische Komplexität trigonometrischer Funktionen mit der technischen Anwendbarkeit in Maschinenbau und Architektur. Diese einzigartige Kombination aus radialsymmetrischer Schönheit und funktionaler Vielseitigkeit macht ihn zu einem unverzichtbaren Element in der modernen Konstruktionstechnik.
Die Geometrie des Keilsektors
Der Zylinderkeil zeigt die Perfektion sektorialer Geometrie:
- Zentralwinkel φ: Bestimmt die Größe des Sektorausschnitts (0° - 180°)
- Winkelabhängige Keillänge: l = r ± √(r² - r²sin²(φ)) je nach Winkelgröße
- Komplexe Volumenformel: Trigonometrische Funktionen in eleganter Kombination
- Radialsymmetrie: Perfekte Symmetrie um die Zylinderachse
- Sektorförmiger Querschnitt: Kreisausschnitt als charakteristische Grundfläche
- Keileffekt: Volumen kleiner als einfacher Kreissektor
- Mantelflächen-Krümmung: Gekrümmte trapezoidale Oberflächengeometrie
Technische Anwendungen
Maschinenbau-Präzision
Keilriemenscheiben und Zahnradsektoren nutzen die präzise Keilgeometrie für optimale Kraftübertragung und minimale Reibungsverluste in Antriebssystemen.
Architektonische Eleganz
Bogenkonstruktionen und Gewölbeelemente verwenden Zylinderkeile für strukturell stabile und ästhetisch ansprechende Bauwerke mit charakteristischer Sektorform.
Rohrleitungs-Innovation
Rohrbogen-Segmente und Flanschkomponenten nutzen die Keilgeometrie für strömungsoptimierte Verbindungen mit minimalen Druckverlusten.
Wissenschaftliche Präzision
Optische Komponenten und Messgeräte-Sektoren verwenden Zylinderkeile für präzise Winkelbestimmungen und Lichtlenkung in wissenschaftlichen Instrumenten.
Zusammenfassung
Der Zylinderkeil verkörpert die perfekte Synthese aus trigonometrischer Komplexität und praktischer Funktionalität. Seine durch den Zentralwinkel φ charakterisierte Form, beschrieben durch die eleganten Formeln für Keillänge l = r ± √(r² - r²sin²(φ)) und das komplexe Volumen V = hr²[3sin(φ)-3φcos(φ)-sin³(φ)]/[3(1-cos(φ))], zeigt die mathematische Raffinesse sektorialer Geometrie. Die winkelabhängige Keillänge und der charakteristische Keileffekt demonstrieren, wie trigonometrische Funktionen praktische Konstruktionslösungen ermöglichen. Von präzisen Keilriemenscheiben über elegante Bogenkonstruktionen bis hin zu strömungsoptimierten Rohrleitungskomponenten - der Zylinderkeil beweist, dass die komplexesten mathematischen Beziehungen oft zu den schönsten und funktionalsten technischen Lösungen führen. Er ist der lebende Beweis dafür, dass sektoriale Geometrie nicht nur mathematische Eleganz besitzt, sondern auch konkrete Anwendungen in der modernen Technik findet und zeigt, wie Winkelgeometrie und Zylinderform in perfekter Harmonie verschmelzen.
|
|
|
|