Bizylinder Rechner
Rechner und Formeln zur Berechnung eines Bizylinders (Steinmetz-Körper)
Bizylinder Rechner
Der Bizylinder
Der Bizylinder ist ein Steinmetz-Körper entstanden durch Schnitt zweier orthogonaler Kreiszylinder.
Bizylinder Eigenschaften
Der Steinmetz-Körper: Schnittvolumen zweier orthogonaler Kreiszylinder
Bizylinder Visualisierung
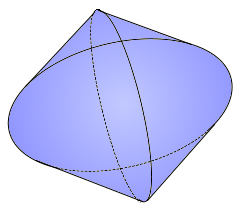
Bizylinder Ansicht
Steinmetz-Körper aus zwei Zylindern

Konstruktion eines Bizylinders
Entstehung durch Zylinderüberschneidung
Van helsing, CC BY-SA 3.0, via Wikimedia Commons
Klassischer Steinmetz-Körper.
Zwei orthogonale Kreiszylinder.
|
|
Was ist ein Bizylinder?
Der Bizylinder (Steinmetz-Körper) ist ein fundamentaler geometrischer Körper:
- Definition: Schnittvolumen zweier orthogonaler Kreiszylinder gleichen Radius
- Name: Nach dem deutschen Mathematiker Jakob Steiner benannt
- Eigenschaften: Hochsymmetrischer Körper mit 6 identischen Flächen
- Konstruktion: Zwei Zylinder schneiden sich rechtwinklig
- Anwendung: Architektur, Maschinenbau, Kristallographie
- Mathematik: Einfache Formeln mit Faktor 16
Geometrische Eigenschaften des Bizylinders
Der Bizylinder zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Radius r: Einheitlicher Radius beider Zylinder
- Orthogonalität: Zylinderachsen stehen senkrecht zueinander
- Schnittachsen: Beide Achsen schneiden sich im Ursprung
- Symmetrie: 3-fache Rotationssymmetrie um jede Achse
Besondere Eigenschaften
- 6 identische Flächen: Jede Fläche ist eine gekrümmte Oberfläche
- Kantenlänge: Alle 12 Kanten haben die Länge 2r
- Spiegelachsen: 9 Spiegelebenen
- Konvexität: Vollständig konvexer Körper
Mathematische Beziehungen des Bizylinders
Der Bizylinder folgt eleganten mathematischen Gesetzen:
Volumen-Formel
Das Volumen ist 16/3 mal der Kubus des Radius. Elegant und einfach zu merken.
Oberflächen-Formel
Die Oberfläche ist 16 mal das Quadrat des Radius. Einfache lineare Beziehung.
Anwendungen des Bizylinders
Bizylinder finden Anwendung in verschiedenen Bereichen:
Architektur & Bau
- Säulenverbindungen
- Kuppelkonstruktionen
- Kreuzungsstrukturen
- Skulpturale Elemente
Maschinenbau & Technik
- Rohrverbindungen
- Gelenkteile
- Maschinenelemente
- 3D-Druck Objekte
Wissenschaft & Forschung
- Kristallographie
- Materialwissenschaft
- Geometrische Studien
- Topologie
Kunst & Design
- Skulpturale Werke
- Möbeldesign
- Schmuckdesign
- Industriedesign
Formeln zum Bizylinder
Volumen (V)
Volumen des Bizylinders in Abhängigkeit vom Radius
Oberfläche (S)
Gesamtoberfläche des Bizylinders
Radius aus Volumen
Radius berechnet aus dem Volumen
Radius aus Oberfläche
Radius berechnet aus der Oberfläche
Bizylinder Eigenschaften
Alle Formeln enthalten 16
Hochsymmetrischer Körper
12 Kanten der Länge 2r
6 identische Oberflächen
Der Bizylinder ist ein mathematisch eleganter und symmetrischer Körper
Berechnungsbeispiel für einen Bizylinder
Gegeben
Gesucht: Volumen und Oberfläche des Bizylinders
1. Volumen-Berechnung
Für r = 5 cm:
\[V = \frac{16}{3} \cdot r^3\] \[V = \frac{16}{3} \cdot 5^3\] \[V = \frac{16}{3} \cdot 125\] \[V = \frac{2000}{3} ≈ 666.67 \text{ cm}^3\]Das Volumen beträgt etwa 666.67 cm³
2. Oberflächen-Berechnung
Für r = 5 cm:
\[S = 16 \cdot r^2\] \[S = 16 \cdot 5^2\] \[S = 16 \cdot 25\] \[S = 400 \text{ cm}^2\]Die Oberfläche beträgt 400 cm²
3. Vergleich mit Kugel
Kugel mit gleichem Radius:
\[V_{Kugel} = \frac{4}{3}\pi r^3 ≈ 523.6 \text{ cm}^3\] \[S_{Kugel} = 4\pi r^2 ≈ 314.2 \text{ cm}^2\]
Verhältnis:
V_Bizylinder / V_Kugel ≈ 1.27
S_Bizylinder / S_Kugel ≈ 1.27
Der Bizylinder ist etwa 27% größer als die Kugel
4. Rückrechnung Kontrolle
Kontrolle aus Volumen:
\[r = \sqrt[3]{\frac{3 \cdot 666.67}{16}}\] \[r = \sqrt[3]{\frac{2000}{16}} = \sqrt[3]{125} = 5 \text{ cm}\]Kontrolle aus Oberfläche:
\[r = \sqrt{\frac{400}{16}} = \sqrt{25} = 5 \text{ cm}\]Beide Rechnungen bestätigen r = 5 cm
5. Zusammenfassung
Der klassische Bizylinder mit allen charakteristischen Eigenschaften
Der Bizylinder: Eleganz der Symmetrie
Der Bizylinder ist ein faszinierender geometrischer Körper, der die Eleganz der Symmetrie und die Schönheit der Geometrie verkörpert. Als Steinmetz-Körper, benannt nach dem deutschen Mathematiker Jakob Steiner, entsteht er durch den Schnitt zweier orthogonaler Kreiszylinder gleichen Radius. Diese einfache Konstruktion führt zu einem hochsymmetrischen Körper mit bemerkenswerten mathematischen Eigenschaften und praktischen Anwendungen in Architektur, Maschinenbau und Kunst.
Die Geometrie der Orthogonalität
Der Bizylinder zeigt die Perfektion orthogonaler Schnitte:
- Orthogonale Konstruktion: Zwei Zylinder schneiden sich rechtwinklig
- Gleicher Radius: Beide Zylinder haben identischen Radius r
- Zentraler Schnitt: Die Zylinderachsen schneiden sich im Zentrum
- 6 identische Flächen: Jede Oberfläche ist eine gekrümmte Fläche
- 12 Kanten: Alle Kanten haben die Länge 2r
- Hochsymmetrie: 9 Spiegelebenen und 3-fache Rotationssymmetrie
- Mathematische Eleganz: Alle Formeln enthalten den Faktor 16
Vielseitige Anwendungen
Architektonische Schönheit
In der Architektur wird der Bizylinder für Säulenverbindungen, Kuppelkonstruktionen und skulpturale Elemente verwendet.
Technische Präzision
Im Maschinenbau findet er Anwendung bei Rohrverbindungen, Gelenkteilen und komplexen Maschinenelementen.
Wissenschaftliche Bedeutung
In der Kristallographie und Materialwissenschaft dient er als Modell für komplexe Strukturen und Symmetrieanalysen.
Künstlerische Inspiration
Als skulpturales Element verkörpert der Bizylinder die perfekte Balance zwischen geometrischer Strenge und ästhetischer Anziehungskraft.
Zusammenfassung
Der Bizylinder verkörpert die perfekte Harmonie zwischen mathematischer Eleganz und praktischer Anwendung. Seine durch orthogonale Zylinderüberschneidung entstehende Form, beschrieben durch elegante Formeln mit dem charakteristischen Faktor 16, macht ihn zu einem fundamentalen Baustein der Geometrie. Von architektonischen Meisterwerken über technische Präzisionsteile bis hin zu künstlerischen Skulpturen - der Bizylinder verbindet theoretische Schönheit mit praktischem Nutzen. Als Steinmetz-Körper zeigt er, wie die einfache Überschneidung zweier Zylinder zu einem der symmetrischsten und elegantesten geometrischen Körper der Mathematik führt, der unsere Welt von der kleinsten technischen Anwendung bis zur größten architektonischen Vision bereichert.
|
|
|
|