Elliptischer Zylinder Rechner
Rechner und Formeln zur Berechnung eines elliptischen Zylinders
Elliptischer Zylinder Rechner
Der elliptische Zylinder
Der elliptische Zylinder ist ein Zylinder mit elliptischer Grundfläche.
Elliptischer Zylinder Eigenschaften
Der elliptische Zylinder: Zylinder mit elliptischer Grundfläche
Elliptischer Zylinder Visualisierung
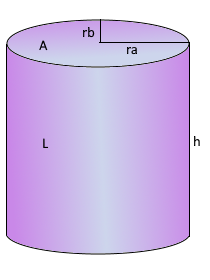
Elliptischer Zylinder
Zylinder mit elliptischer Grundfläche
Parameter
a: Große Halbachse der Ellipse
b: Kleine Halbachse der Ellipse
h: Höhe des Zylinders
Elliptische Grundfläche mit Höhe.
Zwei verschiedene Radien a und b.
|
|
Was ist ein elliptischer Zylinder?
Der elliptische Zylinder ist ein wichtiger geometrischer Körper:
- Definition: Zylinder mit elliptischer statt kreisförmiger Grundfläche
- Parameter: Zwei Halbachsen a und b der Ellipse plus Höhe h
- Eigenschaften: Prismatischer Körper mit konstanter Querschnittsfläche
- Spezialfall: Bei a = b entsteht ein kreisförmiger Zylinder
- Anwendung: Maschinenbau, Architektur, Behältertechnik
- Mathematik: Ramanujan-Näherung für den Ellipsenumfang
Geometrische Eigenschaften des elliptischen Zylinders
Der elliptische Zylinder zeigt charakteristische geometrische Eigenschaften:
Grundparameter
- Halbachse a: Große Halbachse der elliptischen Basis
- Halbachse b: Kleine Halbachse der elliptischen Basis
- Höhe h: Abstand zwischen den beiden Grundflächen
- Elliptizität: Verhältnis e = √(1-b²/a²)
Besondere Eigenschaften
- Prismatisch: Konstante Querschnittsfläche über die Höhe
- Symmetrie: Zwei Symmetrieachsen in der Grundfläche
- Umfang: Exakte Berechnung nur über Elliptische Integrale
- Ramanujan-Formel: Näherung mit Fehler < 0,04%
Mathematische Beziehungen des elliptischen Zylinders
Der elliptische Zylinder folgt eleganten mathematischen Gesetzen:
Volumen-Formel
Das Volumen ist das Produkt aus Ellipsenfläche und Höhe. Einfach und elegant.
Umfang-Formel (Ramanujan)
Ramanujan-Näherung mit maximaler Abweichung von 0,04%. Praktisch exakt für alle Anwendungen.
Anwendungen des elliptischen Zylinders
Elliptische Zylinder finden Anwendung in verschiedenen Bereichen:
Maschinenbau & Technik
- Elliptische Behälter und Tanks
- Rohrleitungen mit ovalem Querschnitt
- Pneumatikzylinder
- Maschinenbauteile
Architektur & Bau
- Elliptische Säulen
- Tunnel mit ovalem Querschnitt
- Brückenelemente
- Moderne Gebäudearchitektur
Wissenschaft & Technik
- Druckkammern und Reaktoren
- Strömungsmechanik
- Medizintechnik
- Optische Systeme
Fahrzeugtechnik
- Kraftstofftanks
- Auspuffanlagen
- Hydraulikzylinder
- Aerodynamische Komponenten
Formeln zum elliptischen Zylinder
Volumen (V)
Volumen des elliptischen Zylinders
Grundfläche (A)
Fläche der elliptischen Basis
Seitenfläche (L)
Mantelfläche des Zylinders
Oberfläche (S)
Gesamtoberfläche des Zylinders
Umfang (P) - Ramanujan-Näherung
\[\text{mit } \lambda = \frac{a-b}{a+b}\]
Ramanujan-Näherung für den Ellipsenumfang mit maximalem Fehler von 0,04%. Diese Formel ist praktisch exakt für alle technischen Anwendungen.
Berechnungsbeispiel für einen elliptischen Zylinder
Gegeben
Gesucht: Alle Parameter des elliptischen Zylinders
1. Grundflächen-Berechnung
Für a = 5 cm, b = 4 cm:
\[A = \pi \cdot a \cdot b\] \[A = \pi \cdot 5 \cdot 4\] \[A = 20\pi ≈ 62.83 \text{ cm}^2\]Die elliptische Grundfläche beträgt etwa 62.83 cm²
2. Volumen-Berechnung
Mit A = 62.83 cm², h = 10 cm:
\[V = A \cdot h = \pi \cdot a \cdot b \cdot h\] \[V = 20\pi \cdot 10\] \[V = 200\pi ≈ 628.32 \text{ cm}^3\]Das Volumen beträgt etwa 628.32 cm³
3. Umfang-Berechnung (Ramanujan)
Ramanujan-Parameter:
\[\lambda = \frac{5-4}{5+4} = \frac{1}{9} ≈ 0.111\] \[\lambda^2 ≈ 0.0123\] \[P ≈ \pi \cdot 9 \cdot \left(1+\frac{3 \cdot 0.0123}{10+\sqrt{4-3 \cdot 0.0123}}\right)\] \[P ≈ 28.38 \text{ cm}\]Der Umfang beträgt etwa 28.38 cm
4. Oberflächen-Berechnung
Seitenfläche und Gesamtoberfläche:
\[L = P \cdot h = 28.38 \cdot 10 ≈ 283.8 \text{ cm}^2\] \[S = 2A + L = 2 \cdot 62.83 + 283.8\] \[S ≈ 409.46 \text{ cm}^2\]Die Gesamtoberfläche beträgt etwa 409.46 cm²
5. Zusammenfassung
Der elliptische Zylinder mit allen charakteristischen Parametern
6. Vergleich mit rundem Zylinder
a=5, b=4, h=10
V≈628.32 cm³
r=4.5, h=10
V≈636.17 cm³
r = √(a·b) ≈ 4.47
≈ 98.8% des Kreises
Der elliptische Zylinder hat etwa das gleiche Volumen wie ein runder Zylinder mit Radius √(a·b)
Der elliptische Zylinder: Eleganz der Ellipse in der dritten Dimension
Der elliptische Zylinder ist ein faszinierender geometrischer Körper, der die Eleganz der Ellipse in die dritte Dimension erweitert. Als Verallgemeinerung des klassischen Kreiszylinders bietet er durch seine zwei verschiedenen Halbachsen eine erhöhte Flexibilität für technische und architektonische Anwendungen. Die mathematische Schönheit liegt in der Kombination aus der einfachen Volumenformel und der komplexeren, aber präzisen Ramanujan-Näherung für den Ellipsenumfang, die praktisch exakte Ergebnisse liefert.
Die Geometrie der Ellipse
Der elliptische Zylinder zeigt die Perfektion elliptischer Geometrie:
- Elliptische Basis: Zwei verschiedene Halbachsen a und b definieren die Grundform
- Prismatische Struktur: Konstante Querschnittsfläche über die gesamte Höhe
- Symmetrieachsen: Zwei orthogonale Symmetrieachsen in der Grundfläche
- Exzentrizität: Maß für die Abweichung von der Kreisform
- Ramanujan-Präzision: Näherungsformel mit Fehler < 0,04%
- Spezialfall Kreis: Bei a = b entsteht der klassische Kreiszylinder
- Praktische Flexibilität: Anpassung an verschiedene Raumverhältnisse
Vielseitige Anwendungen
Technische Überlegenheit
In der Technik ermöglichen elliptische Zylinder optimierte Druckverteilung und Materialausnutzung bei Tanks und Behältern.
Architektonische Eleganz
In der Architektur schaffen elliptische Säulen und Strukturen harmonische Proportionen und effiziente Raumnutzung.
Strömungsoptimierung
Elliptische Profile reduzieren Strömungswiderstand und optimieren die Aerodynamik in Fahrzeugtechnik und Luftfahrt.
Mathematische Schönheit
Die Kombination aus einfacher Volumenformel und präziser Umfangsnäherung zeigt die Eleganz angewandter Mathematik.
Zusammenfassung
Der elliptische Zylinder verkörpert die perfekte Balance zwischen geometrischer Eleganz und praktischer Anwendbarkeit. Seine durch zwei Halbachsen definierte elliptische Grundfläche, erweitert um die dritte Dimension der Höhe, macht ihn zu einem vielseitigen und effizienten geometrischen Körper. Die einfache Volumenformel V = π·a·b·h und die präzise Ramanujan-Näherung für den Umfang zeigen, wie mathematische Eleganz und praktische Brauchbarkeit harmonieren. Von optimierten Druckbehältern über aerodynamische Komponenten bis hin zu architektonischen Meisterwerken - der elliptische Zylinder verbindet die Schönheit der Ellipse mit der Funktionalität der dritten Dimension und beweist, dass Geometrie sowohl ästhetisch ansprechend als auch technisch überlegen sein kann.
|
|
|
|