Frustum Pyramid Calculator
Calculator and formulas to calculate a frustum pyramid
Frustum Pyramid Calculator
The Frustum Pyramid
A frustum pyramid consists of a regular frustum (truncated pyramid) and a pyramid placed on the larger base.
Frustum Pyramid Properties
The composite structure: Combination of frustum and pyramid
Frustum Pyramid Structure
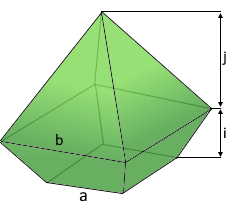
A frustum pyramid with composite structure.
Truncated pyramid with pyramid top.
|
|
What is a Frustum Pyramid?
A frustum pyramid is a fascinating composite polyhedron:
- Definition: A frustum (truncated pyramid) with a pyramid on top
- Structure: Two different base sizes connected
- Components: Frustum base + pyramid top
- Applications: Architecture and engineering
- Complexity: More complex than simple pyramids
- Versatility: Adaptable to various designs
Geometric Properties of Frustum Pyramids
The frustum pyramid exhibits unique geometric properties:
Basic Components
- Frustum: Truncated pyramid with two parallel bases
- Pyramid: Regular pyramid on the larger base
- Heights: Two separate height measurements
- Bases: Two different sizes (a and b)
Special Properties
- Composite: Combination of two geometric forms
- Variable: Adjustable proportions
- Practical: Common in architecture
- Complex: Advanced mathematical relationships
Mathematical Relationships
The frustum pyramid follows complex mathematical laws:
Volume Calculation
Combines frustum and pyramid volumes. Complex but precise calculations.
Surface Area Formula
Includes base, frustum lateral, and pyramid surfaces. Three components combined.
Applications of Frustum Pyramids
Frustum pyramids find applications in various engineering fields:
Architecture & Construction
- Multi-level building structures
- Stepped pyramid designs
- Complex roof systems
- Monument and memorial designs
Engineering & Manufacturing
- Hopper and funnel designs
- Tank and silo structures
- Machine component housings
- Flow control devices
Hydraulic Engineering
- Water treatment facilities
- Settling tanks
- Channel transitions
- Dam spillway structures
Art & Landscape Design
- Sculptural installations
- Garden pyramids and features
- Amphitheater seating
- Modern art structures
Frustum Pyramid Formulas
Overall height (\(\small{h}\))
Total height of frustum and pyramid combined
Base perimeter (\(\small{P}\))
Perimeter of the larger base
Base area (\(\small{A}\))
Area of the smaller base polygon
Lateral surface frustum (\(\small{L_F}\))
Lateral surface area of the frustum part
Surface pyramid (\(\small{L_P}\))
Surface area of the pyramid part
Entire surface (\(\small{S}\))
Total surface area of all parts
Volume frustum (\(\small{V_F}\))
Volume of the frustum part
Volume pyramid (\(\small{V_P}\))
Volume of the pyramid part
Total volume (\(\small{V}\))
Total volume of frustum and pyramid combined
Calculation Example for a Square Frustum Pyramid
Given
Find: All properties of the square frustum pyramid
1. Overall Height Calculation
For i = 4, j = 6:
\[h = i + j\] \[h = 4 + 6 = 10\]The overall height is 10 units
2. Base Area Calculation
For a = 5, n = 4:
\[A = \frac{4 \cdot 5^2}{4 \cdot \tan(\frac{\pi}{4})}\] \[A = \frac{100}{4 \cdot 1} = 25\]The base area is 25 square units
3. Volume Pyramid Calculation
For n = 4, b = 8, j = 6:
\[V_P = \frac{4 \cdot 8^2 \cdot 6}{12 \cdot \tan(\frac{\pi}{4})}\] \[V_P = \frac{1536}{12 \cdot 1} = 128\]The pyramid volume is 128 cubic units
4. The Complete Frustum Pyramid
The square frustum pyramid with perfect engineering proportions
The Frustum Pyramid: Engineering Excellence in Geometry
The frustum pyramid represents one of engineering's most practical and versatile geometric forms. By combining a truncated pyramid (frustum) with a complete pyramid, this composite structure offers unique advantages in architectural design, industrial applications, and structural engineering. The mathematical complexity of frustum pyramids reflects their sophisticated geometry, involving multiple height measurements, different base sizes, and the integration of both frustum and pyramid volume calculations.
The Engineering Marvel of Composite Geometry
The frustum pyramid demonstrates the power of composite geometric design:
- Structural Efficiency: Combines stability of wide base with focused top
- Material Optimization: Efficient use of materials in construction
- Flow Dynamics: Excellent for channeling and directing flows
- Architectural Appeal: Visually striking stepped pyramid design
- Functional Versatility: Adaptable to various engineering needs
- Load Distribution: Superior weight distribution characteristics
- Space Utilization: Maximizes usable volume efficiently
Mathematical Sophistication
Complex Integration
The formulas for frustum pyramids showcase advanced mathematical integration, combining frustum geometry with pyramid calculations through sophisticated trigonometric relationships.
Engineering Precision
The precise calculations required for frustum pyramids reflect their importance in engineering applications where accuracy is critical for structural integrity.
Practical Applications
From water treatment facilities to architectural monuments, frustum pyramids serve practical functions while maintaining aesthetic appeal in modern design.
Design Flexibility
The variable proportions of frustum pyramids allow designers to optimize for specific requirements, balancing function with form.
Summary
The frustum pyramid stands as a testament to the practical application of advanced geometry in engineering and architecture. Its composite structure, combining the stability of a frustum with the elegance of a pyramid, creates a form that is both mathematically sophisticated and practically valuable. The complex formulas governing frustum pyramids reflect their importance in modern engineering, where precise calculations ensure structural integrity and optimal performance. From ancient architectural wonders to contemporary industrial applications, the frustum pyramid continues to demonstrate how mathematical precision can create structures that are both functional and beautiful, serving as bridges between pure geometry and practical engineering solutions.