Frustum Pyramide Rechner
Rechner und Formeln zur Berechnung einer Frustum Pyramide
Frustum Pyramide Rechner
Die Frustum Pyramide
Die Frustum Pyramide ist eine Kombination aus einem Pyramidenstumpf (Frustum) und einer auf die größere Basis aufgesetzten Pyramide.
Frustum Pyramide Eigenschaften
Zusammengesetzter Körper: Pyramidenstumpf mit aufgesetzter Pyramide
Frustum Struktur
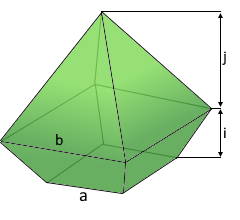
Pyramidenstumpf mit aufgesetzter Pyramide.
Vielseitige zusammengesetzte Struktur.
|
|
Was ist eine Frustum Pyramide?
Die Frustum Pyramide ist ein faszinierender zusammengesetzter geometrischer Körper:
- Definition: Pyramidenstumpf (Frustum) mit aufgesetzter Pyramide
- Struktur: Zwei verschiedene n-eckige Grundflächen
- Komponenten: Unterer Stumpf + obere Pyramide
- Flexibilität: Variable Anzahl von Ecken (n-Eck)
- Anwendung: Architektur und technische Konstruktionen
- Berechnung: Kombination zweier geometrischer Körper
Geometrische Eigenschaften der Frustum Pyramide
Die Frustum Pyramide zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Flächen: n+2 Flächen (2 n-Ecke + n Trapeze)
- Ecken: 2n Ecken (n unten, n oben)
- Kanten: 3n Kanten (n+n Basis, n vertikal)
- Variable: Abhängig von der Eckenzahl n
Besondere Eigenschaften
- Zusammengesetzt: Kombination aus zwei Körpern
- Flexibel: Verschiedene n-Eck Grundrisse möglich
- Praktisch: Häufig in der Architektur verwendet
- Berechenbar: Aufgeteilt in Einzelkomponenten
Mathematische Beziehungen
Die Frustum Pyramide folgt komplexen, aber systematischen mathematischen Gesetzen:
Volumen-Berechnung
Summe aus Frustum-Volumen und Pyramiden-Volumen.
Oberflächen-Berechnung
Kombination aus Basisfläche und verschiedenen Mantelflächen.
Anwendungen der Frustum Pyramide
Frustum Pyramiden finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Moderne Hochhäuser
- Turm- und Spitzenkonstruktionen
- Dachaufbauten
- Skulpturale Gebäudeelemente
Technik & Industrie
- Behälter- und Tankdesign
- Maschinenbaukomponenten
- Trichter und Hopper
- Optische Systeme
Bildung & Forschung
- Geometrie-Studien
- Volumenberechnungen
- 3D-Modellierung
- Mathematische Analysen
Design & Kunst
- Moderne Skulpturen
- Produktdesign
- Möbelgestaltung
- Dekorative Objekte
Formeln zur Frustum Pyramide
Gesamthöhe (h)
Summe aus Frustumhöhe und Pyramidenhöhe
Umfang der Basis (P)
n-faches der größeren Seitenlänge
Basisfläche (A)
Fläche des regelmäßigen n-Ecks
Volumen Pyramide (VP)
Volumen der aufgesetzten Pyramide
Mantelfläche Pyramide (LP)
Mantelfläche der aufgesetzten Pyramide
Gesamte Oberfläche (S)
Summe aller Teilflächen
Mantelfläche Frustum (LF)
Mantelfläche des Pyramidenstumpfs
Volumen Frustum (VF)
Volumen des Pyramidenstumpfs
Gesamtvolumen (V)
Summe aus Frustum- und Pyramidenvolumen
Berechnungsbeispiel für eine Frustum Pyramide
Gegeben
Gesucht: Alle Eigenschaften der Frustum Pyramide (Quadratischer Grundriss)
1. Gesamthöhe-Berechnung
Für i = 4, j = 6:
\[h = i + j\] \[h = 4 + 6\] \[h = 10\]Die Gesamthöhe beträgt 10 Längeneinheiten
2. Basisfläche-Berechnung
Für a = 5, n = 4 (Quadrat):
\[A = \frac{4 \cdot 5^2}{4 \cdot \tan\left(\frac{\pi}{4}\right)}\] \[A = \frac{100}{4 \cdot 1} = 25\]Die Basisfläche beträgt 25 Flächeneinheiten
3. Umfang-Berechnung
Für b = 8, n = 4:
\[P = b \cdot n\] \[P = 8 \cdot 4\] \[P = 32\]Der Basis-Umfang beträgt 32 Längeneinheiten
4. Volumen Pyramide-Berechnung
Für n=4, b=8, j=6:
\[V_P = \frac{4 \cdot 8^2 \cdot 6}{12 \cdot 1}\] \[V_P = \frac{1536}{12} = 128\]Das Pyramidenvolumen beträgt 128 Volumeneinheiten
5. Volumen Frustum-Berechnung
Vereinfachte Berechnung für Quadrat:
\[V_F = \frac{i}{3}(a^2 + ab + b^2)\] \[V_F = \frac{4}{3}(25 + 40 + 64)\] \[V_F = \frac{4 \cdot 129}{3} ≈ 172\]Das Frustumvolumen beträgt etwa 172 Volumeneinheiten
6. Gesamtvolumen-Berechnung
VP ≈ 128, VF ≈ 172:
\[V = V_F + V_P\] \[V = 172 + 128\] \[V = 300\]Das Gesamtvolumen beträgt etwa 300 Volumeneinheiten
Zusammenfassung der Ergebnisse
Die Frustum Pyramide mit quadratischem Grundriss zeigt die Vielseitigkeit zusammengesetzter Körper
Die Frustum Pyramide: Meisterwerk der zusammengesetzten Geometrie
Die Frustum Pyramide repräsentiert eine faszinierende Synthese geometrischer Formen, bei der ein Pyramidenstumpf (Frustum) mit einer aufgesetzten Pyramide zu einem einheitlichen Körper verschmilzt. Diese einzigartige Konstruktion vereint die Stabilität eines Frustums mit der eleganten Spitze einer Pyramide und schafft damit eine vielseitige geometrische Form, die sowohl in der modernen Architektur als auch in technischen Anwendungen häufig zum Einsatz kommt. Die mathematische Berechnung erfordert die systematische Addition der Eigenschaften beider Komponenten.
Die Geometrie der Kombination
Die Frustum Pyramide zeigt die Kunst der geometrischen Komposition:
- Zusammengesetzt: Vereinigung von Pyramidenstumpf und Pyramide
- Variable Basis: Beliebige regelmäßige n-Ecke als Grundriss
- Doppelte Struktur: Zwei verschiedene Höhen und Dimensionen
- Flexible Proportionen: Anpassbare Verhältnisse zwischen den Komponenten
- Praktische Form: Optimale Kombination aus Stabilität und Ästhetik
- Skalierbarkeit: Anwendbar für verschiedene Größenordnungen
- Vielseitigkeit: Geeignet für diverse Anwendungsbereiche
Mathematische Komplexität
Additive Berechnung
Die Frustum Pyramide erfordert die systematische Addition der Volumen und Oberflächen beider Komponenten, was zu komplexen aber eleganten Formeln führt.
Trigonometrische Beziehungen
Die Verwendung von Kotangens-Funktionen ermöglicht die Berechnung für beliebige regelmäßige n-Ecke als Grundriss.
Strukturelle Analyse
Die Kombination zweier geometrischer Körper erfordert präzise Berechnungen der Übergangsflächen und Verbindungsstellen.
Praktische Anwendung
Die Frustum Pyramide verbindet mathematische Theorie mit praktischen Konstruktionsanforderungen in Architektur und Technik.
Zusammenfassung
Die Frustum Pyramide steht als beeindruckendes Beispiel für die Kraft der geometrischen Komposition. Ihre Struktur als Vereinigung von Pyramidenstumpf und Pyramide zeigt, wie mathematische Präzision und praktische Anwendbarkeit harmonisch verschmelzen können. Von modernen Wolkenkratzern bis zu industriellen Behältern demonstriert sie die Vielseitigkeit zusammengesetzter geometrischer Formen. Die komplexen, aber systematischen Berechnungsformeln mit trigonometrischen Funktionen machen sie zu einem faszinierenden Studienobjekt, das zeigt, wie die Kombination einfacher geometrischer Prinzipien zu ausgeklügelten und nützlichen Strukturen führen kann. In der Welt der angewandten Geometrie verkörpert die Frustum Pyramide die perfekte Balance zwischen mathematischer Eleganz und praktischer Funktionalität.
|
|
|
|