Halbzylinder Rechner
Rechner und Formeln zur Berechnung eines Halbzylinders
Halbzylinder Rechner
Der Halbzylinder
Der Halbzylinder ist ein halbierter Kreiszylinder mit halbkreisförmiger Grundfläche.
Halbzylinder Eigenschaften
Der Halbzylinder: Hälfte eines Kreiszylinders mit halbkreisförmiger Basis
Halbzylinder Visualisierung
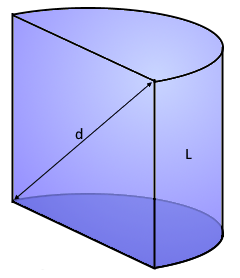
Halbzylinder
Hälfte eines Kreiszylinders
Komponenten
Halbkreis-Grundflächen: 2 × (πr²/2)
Gekrümmte Mantelfläche: πrh
Rechteckige Schnittfläche: 2rh
Halbierter Kreiszylinder.
Genau die Hälfte des Volumens.
|
|
Was ist ein Halbzylinder?
Der Halbzylinder ist ein wichtiger geometrischer Körper:
- Definition: Exakte Hälfte eines Kreiszylinders durch axiale Teilung
- Grundfläche: Zwei halbkreisförmige Endflächen
- Eigenschaften: Gekrümmte Mantelfläche plus ebene Schnittfläche
- Symmetrie: Eine Symmetrieebene durch die Schnittfläche
- Anwendung: Architektur, Rohrleitungen, Dächer
- Mathematik: Einfache Beziehung zum Vollzylinder (Faktor 1/2)
Geometrische Eigenschaften des Halbzylinders
Der Halbzylinder zeigt charakteristische geometrische Eigenschaften:
Grundparameter
- Radius r: Radius der ursprünglichen Kreisbasis
- Höhe h: Abstand zwischen den halbkreisförmigen Endflächen
- Diameter: Durchmesser der Schnittfläche = 2r
- Diagonale: √(h² + (2r)²) durch den ganzen Körper
Besondere Eigenschaften
- Fünf Flächen: 2 Halbkreise + 1 gekrümmte + 1 rechteckige Fläche
- Kanten: 2 gerade Kanten an der Schnittfläche
- Symmetrie: Eine Spiegelebene durch die Längsachse
- Halbierung: Exakt die Hälfte aller Zylinderparameter
Mathematische Beziehungen des Halbzylinders
Der Halbzylinder folgt eleganten mathematischen Gesetzen:
Volumen-Formel
Das Volumen ist exakt die Hälfte eines Vollzylinders. Einfach und logisch.
Oberflächen-Formel
Kombination aus gekrümmter Mantelfläche und zusätzlicher rechteckiger Schnittfläche.
Anwendungen des Halbzylinders
Halbzylinder finden Anwendung in verschiedenen Bereichen:
Architektur & Bau
- Tonnendächer und Gewölbe
- Halbrunde Fenster und Türen
- Brückenelemente
- Tunnel- und U-Bahn-Konstruktionen
Technik & Industrie
- Halbierte Rohrleitungen
- Rinnen und Kanäle
- Schüttgut-Behälter
- Maschinenbau-Komponenten
Wasserbau & Hydraulik
- Halbkreisförmige Kanäle
- Regenrinnen
- Abwasserleitungen
- Bewässerungssysteme
Design & Kunst
- Skulpturale Elemente
- Möbeldesign
- Dekoration und Ornamente
- Landschaftsarchitektur
Formeln zum Halbzylinder
Volumen (V)
Halbes Volumen des entsprechenden Vollzylinders
Mantelfläche (L)
Gekrümmte Mantelfläche (halber Zylinderuumfang)
Gesamtoberfläche (S)
Mantelfläche + Halbkreise + Rechteckfläche
Diagonale (d)
Diagonale durch den gesamten Halbzylinder
Oberflächenaufschlüsselung
\[A_{Halbkreise} = \pi r^2\]
\[A_{Mantel} = \pi r h\]
\[A_{Rechteck} = 2rh\]
\[S = \sum A_i\]
Der Halbzylinder besteht aus fünf verschiedenen Flächenteilen
Berechnungsbeispiel für einen Halbzylinder
Gegeben
Gesucht: Alle Parameter des Halbzylinders
1. Volumen-Berechnung
Für r = 5 cm, h = 12 cm:
\[V = \frac{1}{2} \cdot \pi \cdot r^2 \cdot h\] \[V = \frac{1}{2} \cdot \pi \cdot 5^2 \cdot 12\] \[V = \frac{1}{2} \cdot \pi \cdot 25 \cdot 12\] \[V = 150\pi ≈ 471.24 \text{ cm}^3\]Das Volumen beträgt etwa 471.24 cm³
2. Mantelflächen-Berechnung
Gekrümmte Mantelfläche:
\[L = \pi \cdot r \cdot h\] \[L = \pi \cdot 5 \cdot 12\] \[L = 60\pi ≈ 188.50 \text{ cm}^2\]Die Mantelfläche beträgt etwa 188.50 cm²
3. Oberflächen-Berechnung
Einzelne Flächenkomponenten:
\[A_{Halbkreise} = \pi r^2 = 25\pi ≈ 78.54 \text{ cm}^2\] \[A_{Rechteck} = 2rh = 2 \cdot 5 \cdot 12 = 120 \text{ cm}^2\] \[S = 188.50 + 78.54 + 120 ≈ 387.04 \text{ cm}^2\]Die Gesamtoberfläche beträgt etwa 387.04 cm²
4. Diagonalen-Berechnung
Diagonale durch den Halbzylinder:
\[d = \sqrt{h^2 + (2r)^2}\] \[d = \sqrt{12^2 + 10^2}\] \[d = \sqrt{144 + 100} = \sqrt{244}\] \[d ≈ 15.62 \text{ cm}\]Die Diagonale beträgt etwa 15.62 cm
5. Zusammenfassung
Der Halbzylinder mit allen charakteristischen Parametern
6. Vergleich mit Vollzylinder
r=5, h=12
V≈471.24 cm³
r=5, h=12
V≈942.48 cm³
1 : 2
Exakt die Hälfte
Der Halbzylinder hat exakt das halbe Volumen des entsprechenden Vollzylinders
7. Praktisches Beispiel: Regenrinne
V ≈ 471.24 cm³
≈ 0.47 Liter
S ≈ 387.04 cm²
Blechfläche
Pro Meter: 39.3 L
Bei h=1m
Eine praktische Regenrinne mit r=5cm fasst etwa 39 Liter pro Meter Länge
Der Halbzylinder: Eleganz der halben Symmetrie
Der Halbzylinder ist ein faszinierender geometrischer Körper, der die Eleganz der Zylindersymmetrie mit der Funktionalität einer offenen Struktur verbindet. Als exakte Hälfte eines Kreiszylinders behält er die charakteristischen Eigenschaften der gekrümmten Mantelfläche, erweitert sie aber um die praktische Zugänglichkeit einer ebenen Schnittfläche. Diese Kombination macht ihn zu einem der vielseitigsten und praktischsten geometrischen Körper in Architektur, Technik und Design.
Die Geometrie der Halbierung
Der Halbzylinder zeigt die Perfektion der axialen Teilung:
- Exakte Halbierung: Perfekte Teilung entlang der Zylinderachse
- Halbkreisbasis: Zwei halbkreisförmige Endflächen
- Gekrümmte Mantelfläche: Halber Zylinderumfang über die Höhe
- Rechteckige Schnittfläche: Ebene Fläche mit Länge 2r × h
- Symmetrieebene: Eine Spiegelebene durch die Längsachse
- Einfache Formeln: Alle Parameter mit Faktor 1/2 vom Vollzylinder
- Praktische Öffnung: Zugänglichkeit durch die Schnittfläche
Vielseitige Anwendungen
Architektonische Funktionalität
Tonnendächer und Gewölbekonstruktionen nutzen die strukturelle Stabilität bei optimaler Raumausnutzung und Witterungsschutz.
Hydraulische Effizienz
Halbkreisförmige Kanäle und Rinnen maximieren den Wasserfluss bei minimalen Materialverbrauch und optimaler Selbstreinigung.
Technische Überlegenheit
In der Industrie ermöglichen halbzylindrische Strukturen optimale Materialverteilung und einfache Fertigung bei hoher Belastbarkeit.
Ästhetische Eleganz
Die harmonische Verbindung von gekrümmten und ebenen Flächen schafft ästhetisch ansprechende und funktional optimierte Formen.
Zusammenfassung
Der Halbzylinder verkörpert die perfekte Balance zwischen geometrischer Eleganz und praktischer Funktionalität. Seine durch axiale Halbierung entstehende Form, mit der charakteristischen Kombination aus gekrümmter Mantelfläche und ebener Schnittfläche, macht ihn zu einem der vielseitigsten geometrischen Körper. Die einfachen mathematischen Beziehungen (Faktor 1/2 zum Vollzylinder) bei gleichzeitiger praktischer Zugänglichkeit zeigen, wie elegante Geometrie und technische Brauchbarkeit harmonieren. Von monumentalen Tonnendächern über effiziente Wasserleitungen bis hin zu ästhetischen Designelementen - der Halbzylinder beweist, dass die Halbierung eines geometrischen Körpers oft zu doppelter Funktionalität führt und zeigt, wie die Reduktion auf das Wesentliche zu maximaler Vielseitigkeit werden kann.
|
|
|
|