Siebeneckige Pyramide Rechner
Rechner und Formeln zur Berechnung einer regelmäßigen siebeneckigen Pyramide
Siebeneckpyramide Rechner
Die Regelmäßige Siebeneckpyramide
Eine regelmäßige siebeneckige Pyramide hat ein gleichseitiges Siebeneck als Basis und sieben gleichschenklige Dreiecke als Mantelfläche.
Siebeneckpyramide Eigenschaften
Die mystische Siebeneckpyramide: Ein Siebeneck als Basis mit sieben Dreiecksflächen
Siebeneckpyramide Struktur
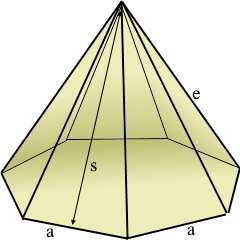
Die regelmäßige Siebeneckpyramide mit mystischer Form.
Siebeneckige Basis mit sieben Dreiecksflächen.
|
|
Was ist eine regelmäßige siebeneckige Pyramide?
Eine regelmäßige siebeneckige Pyramide ist ein faszinierender geometrischer Körper:
- Definition: Pyramide mit regelmäßigem Siebeneck als Basis
- Basis: Gleichseitiges Siebeneck (Heptagon) als Grundfläche
- Mantelflächen: 7 kongruente gleichschenklige Dreiecke
- Ecken: 8 Ecken (7 Basis + 1 Spitze)
- Kanten: 14 Kanten (7 Basis + 7 Seiten)
- Symmetrie: Siebenfache Rotationssymmetrie
Geometrische Eigenschaften der Siebeneckpyramide
Die regelmäßige siebeneckige Pyramide zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Flächen: 8 Flächen (1 Siebeneck + 7 Dreiecke)
- Ecken: 8 Ecken (7 Basis + 1 Apex)
- Kanten: 14 Kanten (7+7)
- Euler-Charakteristik: V - E + F = 8 - 14 + 8 = 2
Besondere Eigenschaften
- Heptagonal: Siebeneckige Symmetrie
- Mystisch: Die Zahl 7 in der Geometrie
- Konvex: Alle Kanten ragen nach außen
- Elegant: Harmonische Proportionen
Mathematische Beziehungen
Die regelmäßige siebeneckige Pyramide folgt eleganten mathematischen Gesetzen:
Volumen-Beziehung
Das Volumen verwendet die heptagonale Grundfläche. Elegant mit π/7-Trigonometrie.
Flächen-Beziehungen
Alle Flächenformeln verwenden π/7 Winkel. Heptagonale Harmonie.
Anwendungen der Siebeneckpyramide
Regelmäßige siebeneckige Pyramiden finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Besondere Dachkonstruktionen
- Symbolische Bauwerke
- Dekorative Turmspitzen
- Moderne Architekturformen
Wissenschaft & Technik
- Spezielle Kristallstrukturen
- Optische Experimente
- Mechanische Komponenten
- Geometrische Studien
Bildung & Lehre
- Geometrie-Unterricht
- Mathematische Demonstrationen
- 3D-Modellierung
- Trigonometrie-Studien
Kunst & Design
- Skulpturale Formen
- Symbolische Objekte
- Produktdesign
- Geometrische Kunstwerke
Formeln zur regelmäßigen siebeneckigen Pyramide
Mantelhöhe (s)
Schräge Höhe mit cot(π/7) ≈ 2.077
Kantenlänge (e)
Länge der Pyramidenkanten
Grundfläche (A)
Fläche des regelmäßigen Siebenecks
Eine Seitenfläche (As)
Fläche eines gleichschenkligen Dreiecks
Mantelfläche (Am)
Gesamtfläche aller Seitenflächen
Oberfläche (S)
Grundfläche plus Mantelfläche
Umfang (P)
Umfang des Siebenecks
Volumen (V)
Ein Drittel von Grundfläche mal Höhe
Berechnungsbeispiel für eine regelmäßige siebeneckige Pyramide
Gegeben
Gesucht: Alle Eigenschaften der Siebeneckpyramide
1. Grundfläche-Berechnung
Siebeneckfläche mit tan(π/7) ≈ 0.481:
\[A = \frac{7 \cdot a^2}{4 \cdot \tan\left(\frac{\pi}{7}\right)}\] \[A = \frac{7 \cdot 64}{4 \cdot 0.481}\] \[A = \frac{448}{1.924} ≈ 232.8\]Die Grundfläche beträgt etwa 232.8 Flächeneinheiten
2. Mantelhöhe-Berechnung
Mit cot(π/7) ≈ 2.077:
\[s = \sqrt{h^2 + \frac{a^2 \cdot \cot^2\left(\frac{\pi}{7}\right)}{4}}\] \[s = \sqrt{100 + \frac{64 \cdot 4.314}{4}}\] \[s = \sqrt{100 + 69.02} ≈ 13.00\]Die Mantelhöhe beträgt etwa 13.00 Einheiten
3. Volumen-Berechnung
Ein Drittel der Basis mal Höhe:
\[V = \frac{A \cdot h}{3}\] \[V = \frac{232.8 \cdot 10}{3}\] \[V ≈ 776.0\]Das Volumen beträgt etwa 776.0 Volumeneinheiten
4. Die perfekte Siebeneckpyramide
Die regelmäßige Siebeneckpyramide mit mystischer Geometrie
Die regelmäßige siebeneckige Pyramide: Das Mysterium der Heptagonalgeometrie
Die regelmäßige siebeneckige Pyramide ist ein außergewöhnlicher geometrischer Körper, der die mystische Kraft der Zahl Sieben mit der eleganten Pyramidenform vereint. Mit einem regelmäßigen Siebeneck (Heptagon) als Basis und sieben kongruenten gleichschenkligen Dreiecken als Mantelflächen verkörpert sie eine seltene und faszinierende geometrische Struktur. Die mathematischen Beziehungen, die durch die trigonometrischen Funktionen des π/7-Winkels geprägt sind, machen sie zu einem herausfordernden und zugleich faszinierenden Studienobjekt der Geometrie.
Die Geometrie der heptagonalen Mystik
Die regelmäßige siebeneckige Pyramide zeigt die Besonderheit der siebenseitigen Symmetrie:
- Heptagonale Basis: Das regelmäßige Siebeneck als seltene Grundform
- Siebenfache Symmetrie: Rotationssymmetrie um 51,43°-Schritte (360°/7)
- Mystische Zahl: Die Zahl 7 in der geometrischen Vollendung
- Transzendente Winkel: π/7 führt zu irrationalen trigonometrischen Werten
- Einzigartige Struktur: Weniger häufig als andere polygonale Pyramiden
- Mathematische Herausforderung: Komplexe trigonometrische Beziehungen
- Symbolische Bedeutung: Die Vollkommenheit der Sieben
Mathematische Eleganz
π/7-Trigonometrie
Alle Formeln der Siebeneckpyramide basieren auf den trigonometrischen Funktionen des π/7-Winkels, der zu faszinierenden irrationalen Werten führt.
Heptagonale Mathematik
Die siebeneckige Basis folgt den besonderen Gesetzen der heptagonalen Geometrie, die in der Mathematik eine Sonderstellung einnimmt.
Symbolische Perfektion
Die Zahl Sieben gilt in vielen Kulturen als vollkommen und mystisch, was der Siebeneckpyramide eine besondere symbolische Bedeutung verleiht.
Konstruktive Herausforderung
Die Konstruktion eines regelmäßigen Siebenecks mit Zirkel und Lineal ist unmöglich, was diese Pyramide zu einer besonderen geometrischen Form macht.
Zusammenfassung
Die regelmäßige siebeneckige Pyramide verkörpert die perfekte Verbindung zwischen mathematischer Komplexität und geometrischer Schönheit. Ihre heptagonale Basis und die sieben gleichschenkligen Dreiecksflächen, beschrieben durch die faszinierenden π/7-Trigonometriebeziehungen, machen sie zu einem der interessantesten Studienobjekte der Geometrie. Obwohl sie seltener auftritt als andere polygonale Pyramiden, zeigt die Siebeneckpyramide die mathematische Schönheit der irrationalen Werte und die symbolische Kraft der Zahl Sieben. Von der reinen Mathematik bis zur symbolischen Bedeutung bleibt die siebeneckige Pyramide ein faszinierendes Beispiel für die Tiefe und Komplexität der dreidimensionalen Geometrie.
|
|
|
|