Sechseckige Doppelpyramide Rechner
Rechner und Formeln zur Berechnung einer regelmäßigen sechseckigen Doppelpyramide
Sechseck-Doppelpyramide Rechner
Die sechseckige Doppelpyramide
Die sechseckige Doppelpyramide besteht aus 12 gleichschenkligen Dreiecken um ein regelmäßiges Sechseck als Basis.
Sechseck-Doppelpyramide Eigenschaften
Die doppelte Sechseck-Pyramide: Zwei Pyramiden an der Sechseckbasis verbunden
Sechseck-Doppelpyramide Struktur
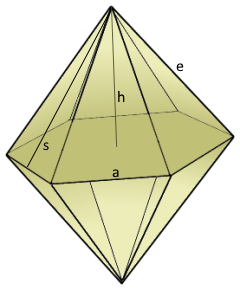
Die sechseckige Doppelpyramide mit perfekter Symmetrie.
12 gleichschenklige Dreiecke um ein Sechseck.
|
|
Was ist eine sechseckige Doppelpyramide?
Die sechseckige Doppelpyramide ist ein faszinierender geometrischer Körper:
- Definition: Zwei Pyramiden an einer Sechseckbasis verbunden
- Basis: Regelmäßiges Sechseck als zentrale Grundfläche
- Flächen: 12 kongruente gleichschenklige Dreiecke
- Ecken: 8 Ecken (6 äquatorial, 2 polar)
- Kanten: 18 Kanten (6+6+6)
- Symmetrie: Perfekte D6h-Symmetrie
Geometrische Eigenschaften der Sechseck-Doppelpyramide
Die sechseckige Doppelpyramide zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Flächen: 12 gleichschenklige Dreiecke
- Ecken: 8 Ecken (6 äquatorial, 2 polar)
- Kanten: 18 Kanten (alle gleich lang)
- Euler-Charakteristik: V - E + F = 8 - 18 + 12 = 2
Besondere Eigenschaften
- Deltaeder: Alle Flächen sind Dreiecke
- Bipyramide: Zwei gespiegelte Pyramiden
- Sechseck-Basis: Perfekte Sechsseitigkeit
- Konvex: Keine einspringenden Kanten
Mathematische Beziehungen
Die sechseckige Doppelpyramide folgt eleganten mathematischen Gesetzen:
Volumen-Formel
Verwendet die Tangens-Funktion für π/6. Elegant und präzise.
Oberflächen-Formel
12 gleichschenklige Dreiecke. Sechsfache Symmetrie.
Anwendungen der Sechseck-Doppelpyramide
Sechseckige Doppelpyramiden finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Kirchturmspitzen und Türme
- Dekorative Dachelemente
- Strukturelle Verstrebungen
- Skulpturale Baukomponenten
Wissenschaft & Technik
- Kristallographische Strukturen
- Molekulare Geometrie
- Optische Prismen
- Mechanische Komponenten
Bildung & Lehre
- Geometrie-Unterricht
- 3D-Geometrie-Studien
- Symmetrie-Demonstrationen
- Polyeder-Klassifikation
Kunst & Design
- Geometrische Skulpturen
- Moderne Kunstwerke
- Dekorative Objekte
- Schmuckdesign
Formeln zur sechseckigen Doppelpyramide
Mantelhöhe (s)
Schräge Höhe mit Kotangens π/6 = √3
Kantenlänge (e)
Länge der Doppelpyramiden-Kanten
Gesamthöhe (i)
Doppelte Höhe der Einzelpyramide
Eine Seitenfläche (As)
Fläche eines gleichschenkligen Dreiecks
Oberfläche (S)
12 gleichschenklige Dreiecksflächen
Umfang (P)
Umfang des Sechsecks
Volumen (V)
Mit √3 Faktor durch tan(π/6) = 1/√3
Berechnungsbeispiel für eine sechseckige Doppelpyramide
Gegeben
Gesucht: Alle Eigenschaften der sechseckigen Doppelpyramide
1. Mantelhöhe-Berechnung
Für Sechseck (cot(π/6) = √3):
\[s = \sqrt{12^2 + \frac{6^2 \cdot (\sqrt{3})^2}{4}}\] \[s = \sqrt{144 + \frac{36 \cdot 3}{4}}\] \[s = \sqrt{144 + 27} = \sqrt{171} ≈ 13.08\]Die Mantelhöhe beträgt etwa 13.08 Einheiten
2. Volumen-Berechnung
Mit √3 Faktor:
\[V = a^2 \cdot h \cdot \sqrt{3}\] \[V = 6^2 \cdot 12 \cdot \sqrt{3}\] \[V = 36 \cdot 12 \cdot 1.732 ≈ 748.2\]Das Volumen beträgt etwa 748.2 Volumeneinheiten
3. Oberflächen-Berechnung
12 Dreiecke:
\[S = 6 \cdot a \cdot s\] \[S = 6 \cdot 6 \cdot 13.08\] \[S ≈ 470.9\]Die Oberfläche beträgt etwa 470.9 Flächeneinheiten
4. Die perfekte Sechseck-Doppelpyramide
Die sechseckige Doppelpyramide mit perfekter Symmetrie
Die sechseckige Doppelpyramide: Die Perfektion der Sechsseitigkeit
Die sechseckige Doppelpyramide ist ein faszinierender geometrischer Körper, der die Eleganz der perfekten Sechsseitigkeit verkörpert. Durch die Verbindung zweier Pyramiden an einer regelmäßigen Sechseckbasis entsteht eine einzigartige Struktur mit 12 kongruenten gleichschenkligen Dreiecken, die diesen Körper zu einem der schönsten Beispiele für geometrische Symmetrie macht. Die mathematische Schönheit liegt in den eleganten Beziehungen mit der Quadratwurzel von 3 und den trigonometrischen Funktionen des 60°-Winkels, die alle geometrischen Eigenschaften harmonisch verbinden.
Die Geometrie der Sechsseitigkeit
Die sechseckige Doppelpyramide zeigt die Perfektion der sechsseitigen Symmetrie:
- Deltaeder: Alle 12 Flächen sind kongruente gleichschenklige Dreiecke
- D6h-Symmetrie: Sechszählige Rotationssymmetrie mit Spiegelebene
- Bipyramide: Zwei gespiegelte Pyramiden mit Sechseckbasis
- Sechseck-Perfektion: Das regelmäßige Sechseck als ideale Basis
- Konvexität: Alle Ecken ragen nach außen
- Uniformität: Alle Seitenkanten haben dieselbe Länge
- Eleganz: Harmonische Proportionen durch √3-Beziehungen
Mathematische Eleganz
Quadratwurzel-3-Perfektion
Die Formeln der sechseckigen Doppelpyramide sind Meisterwerke der Einfachheit, mit √3 als zentralem Faktor durch cot(π/6) = √3 und tan(π/6) = 1/√3.
Sechseck-Verwandtschaft
Das regelmäßige Sechseck als Basis zeigt die natürliche Verwandtschaft zur hexagonalen Kristallstruktur und Bienenwaben-Geometrie.
Strukturelle Perfektion
Die perfekte Sechsseitigkeit und Stabilität machen die Doppelpyramide zu einer bevorzugten Form in Natur und Technik.
Ästhetische Vollendung
Die harmonische Vereinigung zweier Pyramiden über einem Sechseck erzeugt eine einzigartige visuelle Balance und natürliche Schönheit.
Zusammenfassung
Die sechseckige Doppelpyramide verkörpert die perfekte Balance zwischen mathematischer Eleganz und geometrischer Schönheit. Ihre Struktur aus zwölf gleichschenkligen Dreiecken, beschrieben durch die elegante √3-Beziehung, macht sie zu einem faszinierenden Studienobjekt für Mathematiker, Architekten und Designer. Die natürliche Verwandtschaft zum regelmäßigen Sechseck zeigt die universelle Bedeutung der Sechsseitigkeit in Natur und Technik. Von der Kristallographie bis zur modernen Architektur bleibt die sechseckige Doppelpyramide ein faszinierendes Beispiel für die Kraft der geometrischen Symmetrie und die Schönheit der mathematischen Harmonie in drei Dimensionen.
|
|
|
|