Hohlzylinder Rechner
Rechner und Formeln zur Berechnung eines Hohlzylinders
Hohlzylinder Rechner
Der Hohlzylinder
Der Hohlzylinder ist ein hohler Kreiszylinder mit Außen- und Innenradius.
Hohlzylinder Eigenschaften
Der Hohlzylinder: Hohler Kreiszylinder mit Außen- und Innenradius
Hohlzylinder Visualisierung
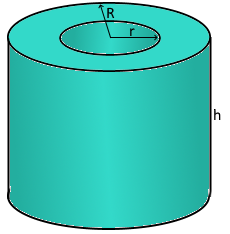
Hohlzylinder
Röhrenförmiger Körper mit Hohlraum
Komponenten
R: Außenradius (äußere Begrenzung)
r: Innenradius (Hohlraum)
h: Höhe des Zylinders
Hohler Kreiszylinder.
Materialersparnis durch Hohlraum.
|
|
Was ist ein Hohlzylinder?
Der Hohlzylinder ist ein wichtiger geometrischer Körper:
- Definition: Hohlzylinder mit kreisförmigem Querschnitt und zentralem Hohlraum
- Parameter: Außenradius R, Innenradius r und Höhe h
- Eigenschaften: Röhrenförmiger Körper mit konstanter Wandstärke
- Wandstärke: t = R - r (Differenz der Radien)
- Anwendung: Rohre, Schläuche, Säulen, Behälter
- Mathematik: Differenz zweier Zylinder (R² - r²)
Geometrische Eigenschaften des Hohlzylinders
Der Hohlzylinder zeigt charakteristische geometrische Eigenschaften:
Grundparameter
- Außenradius R: Radius der äußeren Begrenzung
- Innenradius r: Radius des zentralen Hohlraums
- Höhe h: Abstand zwischen den Ringflächen
- Wandstärke t: t = R - r (Materialdicke)
Besondere Eigenschaften
- Vier Flächen: 2 Ringflächen + Außen- + Innenmantelfläche
- Rotationssymmetrie: Symmetrie um die Mittelachse
- Materialersparnis: Hohlraum reduziert Materialverbrauch
- Strukturelle Effizienz: Hohe Stabilität bei geringem Gewicht
Mathematische Beziehungen des Hohlzylinders
Der Hohlzylinder folgt eleganten mathematischen Gesetzen:
Volumen-Formel
Das Volumen ist die Differenz zweier Zylinder. Elegante Subtraktion.
Oberflächen-Formel
Kombination aus Ringflächen und beiden Mantelflächen (innen und außen).
Anwendungen des Hohlzylinders
Hohlzylinder finden Anwendung in verschiedenen Bereichen:
Rohrleitungstechnik
- Wasserleitungen und Abwasserrohre
- Gasleitungen und Dampfrohre
- Hydraulik- und Pneumatikleitungen
- Chemische Prozessrohre
Bauwesen & Architektur
- Hohle Stützsäulen
- Kabelkanäle und -rohre
- Lüftungsschächte
- Architektonische Elemente
Maschinenbau & Automotive
- Zylinderbuchsen und Hülsen
- Auspuffrohre und Schalldämpfer
- Hydraulikzylinder
- Lager- und Führungsbuchsen
Verfahrenstechnik
- Reaktionsrohre
- Wärmetauscher
- Destillationskolonnen
- Bioreaktor-Behälter
Formeln zum Hohlzylinder
Volumen (V)
Volumen als Differenz zwischen äußerem und innerem Zylinder
Basisfläche (A)
Ringfläche der Grundfläche
Seitenflächen (L)
Summe aus Außen- und Innenmantelfläche
Gesamtoberfläche (S)
Zwei Ringflächen plus Mantelflächen
Einzelne Mantelflächen
\[L_o = 2\pi Rh\]
\[L_i = 2\pi rh\]
\[t = R - r\]
Der Hohlzylinder besteht aus vier verschiedenen Oberflächenteilen
Umkehrformeln
\[h = \frac{V}{\pi(R^2-r^2)}\]
\[P = 2\pi r\]
Nützliche Umkehrformeln für die Praxis
Berechnungsbeispiel für einen Hohlzylinder
Gegeben
Gesucht: Alle Parameter des Hohlzylinders
1. Volumen-Berechnung
Für R = 5 cm, r = 4 cm, h = 10 cm:
\[V = \pi \cdot (R^2 - r^2) \cdot h\] \[V = \pi \cdot (5^2 - 4^2) \cdot 10\] \[V = \pi \cdot (25 - 16) \cdot 10\] \[V = 90\pi ≈ 282.74 \text{ cm}^3\]Das Volumen beträgt etwa 282.74 cm³
2. Basisflächen-Berechnung
Ringfläche (eine Basis):
\[A = \pi \cdot (R^2 - r^2)\] \[A = \pi \cdot (25 - 16)\] \[A = 9\pi ≈ 28.27 \text{ cm}^2\]Eine Ringfläche beträgt etwa 28.27 cm²
3. Mantelflächen-Berechnung
Einzelne Mantelflächen:
\[L_o = 2\pi \cdot 5 \cdot 10 = 100\pi ≈ 314.16 \text{ cm}^2\] \[L_i = 2\pi \cdot 4 \cdot 10 = 80\pi ≈ 251.33 \text{ cm}^2\] \[L = L_o + L_i ≈ 565.49 \text{ cm}^2\]Die gesamten Mantelflächen betragen etwa 565.49 cm²
4. Gesamtoberfläche
Alle Oberflächen zusammen:
\[S = 2A + L\] \[S = 2 \cdot 28.27 + 565.49\] \[S = 56.54 + 565.49\] \[S ≈ 622.03 \text{ cm}^2\]Die Gesamtoberfläche beträgt etwa 622.03 cm²
5. Zusätzliche Parameter
t = R - r = 1 cm
P = 2πr ≈ 25.13 cm
Po = 2πR ≈ 31.42 cm
rm = (R+r)/2 = 4.5 cm
Weitere nützliche Parameter des Hohlzylinders
6. Zusammenfassung
Der Hohlzylinder mit allen charakteristischen Parametern
7. Praktisches Beispiel: Wasserrohr
V ≈ 282.74 cm³
≈ 0.28 Liter
S ≈ 622.03 cm²
Rohroberfläche
Querschnitt: 28.27 cm²
Für Strömungsberechnungen
Ein Wasserrohr mit diesen Dimensionen fasst etwa 0.28 Liter pro 10 cm Länge
8. Vergleich mit Vollzylinder
R=5, r=4, h=10
V≈282.74 cm³
r=5, h=10
V≈785.40 cm³
≈ 64% weniger Volumen
Effizienter!
Der Hohlzylinder spart etwa 64% Material gegenüber einem Vollzylinder gleicher Außenmaße
Der Hohlzylinder: Perfektion der Materialeffizienz
Der Hohlzylinder ist ein faszinierender geometrischer Körper, der die perfekte Balance zwischen struktureller Stabilität und Materialeffizienz verkörpert. Als hohler Kreiszylinder mit zentral ausgespartem Volumen bietet er bei minimaler Materialverwendung maximale Funktionalität. Diese einzigartige Eigenschaft macht ihn zu einem der wichtigsten und vielseitigsten geometrischen Körper in Technik, Architektur und Ingenieurswesen, wo Gewichtsersparnis und Kosteneffizienz entscheidend sind.
Die Geometrie der Effizienz
Der Hohlzylinder zeigt die Perfektion struktureller Optimierung:
- Doppelte Radien: Außenradius R und Innenradius r definieren die Form
- Materialersparnis: Zentraler Hohlraum reduziert Materialverbrauch
- Strukturelle Effizienz: Hohe Stabilität bei geringem Gewicht
- Vier Oberflächen: Außen- und Innenmantelfläche plus zwei Ringflächen
- Wandstärke t = R - r: Definiert die Materialdicke
- Rotationssymmetrie: Perfekte Symmetrie um die Mittelachse
- Vielseitige Anwendung: Von Rohrleitungen bis zu Architektur
Technische Überlegenheit
Rohrleitungstechnik
Als Grundform aller Rohrleitungen ermöglicht der Hohlzylinder effizienten Transport von Flüssigkeiten, Gasen und anderen Medien bei optimaler Materialausnutzung.
Struktureller Leichtbau
In der Architektur und im Bauwesen bieten hohle Stützen und Säulen maximale Tragfähigkeit bei minimalem Eigengewicht und Materialverbrauch.
Maschinenbau-Innovation
Zylinderbuchsen, Führungshülsen und Lagerbuchsen nutzen die präzise Geometrie für optimale Funktion bei reduziertem Materialaufwand.
Verfahrenstechnische Perfektion
Reaktionsrohre und Wärmetauscher maximieren die Oberflächen-zu-Volumen-Ratio für optimale Wärme- und Stoffübertragung.
Zusammenfassung
Der Hohlzylinder verkörpert die perfekte Synthese aus geometrischer Eleganz und technischer Effizienz. Seine durch den zentralen Hohlraum charakterisierte Form, beschrieben durch die elegante Differenzformel π(R²-r²)h, macht ihn zum Inbegriff intelligenter Materialverwendung. Die Kombination aus struktureller Stabilität, Gewichtsersparnis und vielseitiger Anwendbarkeit zeigt, wie mathematische Präzision und praktische Notwendigkeit harmonieren. Von lebensnotwendigen Wasserleitungen über tragende Architekturelemente bis hin zu präzisen Maschinenbauteilen - der Hohlzylinder beweist, dass weniger oft mehr ist und demonstriert, wie die Kunst des Weglassens zu maximaler Funktionalität führt. Er ist der geometrische Beweis dafür, dass Effizienz und Eleganz untrennbar miteinander verbunden sind.
|
|
|
|