Hyperboloid Rechner
Rechner und Formeln zur Berechnung eines Hyperboloids
Hyperboloid Rechner
Das Hyperboloid
Das Hyperboloid ist eine hyperbolische Rotationsfläche mit charakteristischer Taillenform.
Hyperboloid Eigenschaften
Das Hyperboloid: Rotationsfläche einer Hyperbel um ihre Symmetrieachse
Hyperboloid Visualisierung
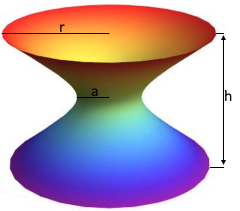
Hyperboloid
Rotationsfläche mit charakteristischer Taillenform
Parameter
r: Basisradius (größter Radius)
a: Mittelradius (Taille)
h: Gesamthöhe
Bild von Anton Sel, CC BY-SA 4.0, via Wikimedia Commons
Hyperbolische Rotationsfläche.
Mathematische Eleganz in 3D.
|
|
Was ist ein Hyperboloid?
Das Hyperboloid ist ein faszinierender geometrischer Körper:
- Definition: Rotationsfläche einer Hyperbel um ihre Symmetrieachse
- Form: Charakteristische Taillenform mit schmalster Stelle in der Mitte
- Parameter: Basisradius r, Mittelradius a und Höhe h
- Typ: Einschaliges Hyperboloid (Hyperboloid of one sheet)
- Anwendung: Architektur, Ingenieurbau, Kühlturmkonstruktion
- Mathematik: Quadratische Gleichung in drei Variablen
Geometrische Eigenschaften des Hyperboloids
Das Hyperboloid zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Basisradius r: Größter Radius an den Enden
- Mittelradius a: Kleinster Radius in der Taille
- Höhe h: Gesamthöhe des Hyperboloids
- Formparameter c: Bestimmt die Krümmung der Hyperbel
Besondere Eigenschaften
- Rotationssymmetrie: Symmetrie um die vertikale Achse
- Hyperbolische Meridiane: Jeder Meridianschnitt ist eine Hyperbel
- Kreisförmige Querschnitte: Alle horizontalen Schnitte sind Kreise
- Regelflächeneigenschaft: Kann durch gerade Linien erzeugt werden
Mathematische Beziehungen des Hyperboloids
Das Hyperboloid folgt eleganten mathematischen Gesetzen:
Volumen-Formel
Das Volumen kombiniert beide Radien in eleganter Weise. Mathematische Schönheit.
Formparameter c
Der Formparameter bestimmt die Krümmung der hyperbolischen Form.
Anwendungen des Hyperboloids
Hyperboloide finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Kühlturmkonstruktionen
- Moderne Hochhäuser und Türme
- Brückenelemente und Tragwerke
- Schalenbauten und Kuppeln
Ingenieurswesen
- Dampfturbinen und Rotoren
- Aerodynamische Komponenten
- Druckbehälter und Reaktoren
- Strömungsführende Bauteile
Wissenschaft & Forschung
- Teilchenbeschleuniger
- Optische Systeme
- Astronomische Instrumente
- Materialwissenschaft
Kunst & Design
- Skulpturale Werke
- Architektonische Highlights
- Industriedesign
- Mathematische Kunst
Formeln zum Hyperboloid
Volumen (V)
Volumen des einschaligen Hyperboloids
Formparameter (c)
Parameter zur Beschreibung der hyperbolischen Krümmung
Basisradius aus a und c
Rückrechnung des Basisradius
Hyperbolische Gleichung
Standardform des einschaligen Hyperboloids
Hyperboloid Eigenschaften
Einschaliges Hyperboloid
Hyperbolisch
Rotationssymmetrisch
Kreisförmig
Das Hyperboloid kombiniert hyperbolische Krümmung mit rotationssymmetrischer Eleganz
Berechnungsbeispiel für ein Hyperboloid
Gegeben
Gesucht: Volumen und Formparameter des Hyperboloids
1. Volumen-Berechnung
Für r = 8 cm, a = 4 cm, h = 10 cm:
\[V = \frac{1}{3} \cdot \pi \cdot h \cdot (2a^2 + r^2)\] \[V = \frac{1}{3} \cdot \pi \cdot 10 \cdot (2 \cdot 16 + 64)\] \[V = \frac{1}{3} \cdot \pi \cdot 10 \cdot (32 + 64)\] \[V = \frac{1}{3} \cdot \pi \cdot 10 \cdot 96 = 320\pi ≈ 1005.31 \text{ cm}^3\]Das Volumen beträgt etwa 1005.31 cm³
2. Formparameter-Berechnung
Berechnung des Parameters c:
\[\frac{r^2}{a^2} = \frac{64}{16} = 4\] \[\frac{r^2}{a^2} - 1 = 4 - 1 = 3\] \[c = \sqrt{\frac{h^2}{4 \cdot 3}} = \sqrt{\frac{100}{12}} = \sqrt{8.333}\] \[c ≈ 2.89 \text{ cm}\]Der Formparameter c beträgt etwa 2.89 cm
3. Geometrische Analyse
Geometrische Kennwerte:
Taillenverhältnis:\[\frac{a}{r} = \frac{4}{8} = 0.5\] Höhen-Radius-Verhältnis:
\[\frac{h}{r} = \frac{10}{8} = 1.25\] Krümmungsparameter:
\[\frac{c}{a} = \frac{2.89}{4} ≈ 0.72\]
Das Hyperboloid hat eine deutliche Taillenform
4. Kontrollrechnung
Rückrechnung des Basisradius:
\[r = a \cdot \sqrt{1 + \frac{h^2}{4c^2}}\] \[r = 4 \cdot \sqrt{1 + \frac{100}{4 \cdot 8.333}}\] \[r = 4 \cdot \sqrt{1 + 3} = 4 \cdot 2 = 8 \text{ cm}\]Die Kontrollrechnung bestätigt r = 8 cm
5. Zusammenfassung
Das Hyperboloid mit charakteristischer Taillenform und allen Parametern
6. Praktisches Beispiel: Kühlturm
V ≈ 1005.31 cm³
≈ 1.01 Liter
Taille: 50% des Basisradius
Materialersparnis
Hyperbolische Form
Optimaler Luftzug
Ein Kühlturm mit hyperbolischer Form optimiert Strömung und Materialverbrauch
7. Vergleich mit Zylinder
r=8, a=4, h=10
V≈1005.31 cm³
r=8, h=10
V≈2010.62 cm³
≈ 50% des Zylindervolumens
Effizienter!
Das Hyperboloid hat etwa die Hälfte des Volumens eines entsprechenden Zylinders
Das Hyperboloid: Mathematische Eleganz in der Architektur
Das Hyperboloid ist eine der faszinierendsten geometrischen Formen, die mathematische Eleganz mit praktischer Funktionalität vereint. Als Rotationsfläche einer Hyperbel um ihre Symmetrieachse entsteht eine charakteristische Taillenform, die nicht nur ästhetisch ansprechend ist, sondern auch strukturelle und strömungstechnische Vorteile bietet. Diese einzigartige Kombination aus mathematischer Präzision und praktischem Nutzen macht das Hyperboloid zu einem bevorzugten Element in der modernen Architektur und im Ingenieurbau.
Die Geometrie der Hyperbel
Das Hyperboloid zeigt die Perfektion hyperbolischer Geometrie:
- Hyperbolische Meridiane: Jeder vertikale Schnitt zeigt eine Hyperbel
- Kreisförmige Querschnitte: Alle horizontalen Schnitte sind perfekte Kreise
- Taillenform: Schmalste Stelle in der Mitte bei Radius a
- Rotationssymmetrie: Unendlich viele Symmetrieebenen durch die Achse
- Regelflächeneigenschaft: Kann durch gerade Linien erzeugt werden
- Parametrische Beschreibung: Elegante mathematische Formeln
- Quadratische Gleichung: x²/a² + y²/a² - z²/c² = 1
Architektonische Meisterwerke
Kühlturm-Revolution
Hyperbolische Kühltürme optimieren Luftströmung und Materialverbrauch durch ihre charakteristische Taillenform und schaffen ikonische Silhouetten.
Strukturelle Überlegenheit
Die hyperbolische Form bietet optimale Lastverteilung und Stabilität bei minimalem Materialaufwand in Hochhäusern und Türmen.
Strömungsoptimierung
In der Ingenieurstechnik ermöglichen hyperbolische Profile optimale Strömungsführung in Turbinen, Düsen und aerodynamischen Komponenten.
Ästhetische Innovation
Als skulpturales Element verkörpert das Hyperboloid die perfekte Synthese aus mathematischer Präzision und künstlerischer Ausdruckskraft.
Zusammenfassung
Das Hyperboloid verkörpert die perfekte Harmonie zwischen mathematischer Eleganz und praktischer Funktionalität. Seine durch hyperbolische Rotation entstehende Taillenform, beschrieben durch die elegante Volumenformel V = (π/3)h(2a²+r²), macht es zu einem der vielseitigsten und effizientesten geometrischen Körper. Die Kombination aus struktureller Stabilität, Materialersparnis und strömungsoptimalen Eigenschaften zeigt, wie mathematische Präzision praktische Vorteile schafft. Von den ikonischen Kühltürmen der Kraftwerke über moderne Wolkenkratzer bis hin zu präzisen Turbinenschaufeln - das Hyperboloid beweist, dass die schönsten geometrischen Formen oft auch die funktionalsten sind. Es ist der lebende Beweis dafür, dass Mathematik nicht nur abstrakte Schönheit besitzt, sondern auch konkrete Lösungen für komplexe technische Herausforderungen bietet und dabei ästhetische Meisterwerke erschafft, die unsere gebaute Umwelt prägen.
|
|
|
|