Dreieckige Doppelpyramide Rechner
Rechner und Formeln zur Berechnung einer regelmäßigen dreieckigen Doppelpyramide
Dreieckige Doppelpyramide Rechner
Die Dreieckige Doppelpyramide
Eine dreieckige Doppelpyramide besteht aus zwei Pyramiden mit gemeinsamer gleichseitiger dreieckiger Grundfläche.
Dreieckige Doppelpyramide Eigenschaften
Symmetrische Struktur: Zwei Pyramiden mit gemeinsamer gleichseitiger Dreiecksbasis
Dreieckige Doppelpyramide Struktur
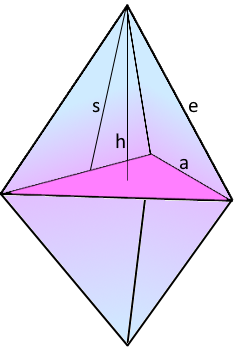
Dreieckige Doppelpyramide mit gleichseitiger Dreiecksbasis.
Symmetrische Pyramiden-Kombination.
|
|
Was ist eine dreieckige Doppelpyramide?
Die dreieckige Doppelpyramide ist eine elegante geometrische Struktur:
- Definition: Zwei kongruente Pyramiden mit gemeinsamer Dreiecksbasis
- Basis: Gleichseitiges Dreieck als Mittelebene
- Flächen: 6 kongruente Dreiecks-Seitenflächen
- Ecken: 3 äquatoriale + 2 polare Ecken
- Kanten: 9 Kanten (3 Grund + 6 Seiten)
- Symmetrie: Perfekte C3v-Symmetrie
Geometrische Eigenschaften der dreieckigen Doppelpyramide
Die dreieckige Doppelpyramide zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Flächen: 6 kongruente Dreiecke
- Ecken: 3 äquatoriale + 2 polare Ecken
- Kanten: 9 Kanten insgesamt
- Euler-Charakteristik: V - E + F = 5 - 9 + 6 = 2
Besondere Eigenschaften
- Deltaeder: Alle Flächen sind Dreiecke
- Gleichseitig: Basis ist gleichseitiges Dreieck
- Symmetrisch: Perfekte Spiegelsymmetrie
- Konvex: Keine einspringenden Kanten oder Ecken
Mathematische Beziehungen
Die dreieckige Doppelpyramide folgt eleganten trigonometrischen Gesetzen:
Volumen-Formel
Enthält die √3 Tangens-Funktion für gleichseitige Dreiecke. Spezifisch für dreieckige Grundflächen.
Mantelhöhen-Formel
Kotangens von 60° für Dreieck-Geometrie. Pythagoras für Raumdiagonalen.
Anwendungen der dreieckigen Doppelpyramide
Dreieckige Doppelpyramiden finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Dreieckige Dachkonstruktionen
- Pyramidale Turmspitzen
- Strukturelle Verstrebungen
- Moderne dreieckige Architektur
Wissenschaft & Technik
- Kristallographische Strukturen
- Molekulare Doppelpyramid-Geometrie
- Optische Dreieck-Prismen
- Mechanische Verbindungselemente
Bildung & Lehre
- Geometrie-Unterricht und -Studien
- 3D-Geometrie-Demonstrationen
- Dreieck-Geometrie Anwendungen
- Trigonometrie-Beispiele
Kunst & Design
- Geometrische Skulpturen
- Dreieckige Kunstinstallationen
- Dekorative Designobjekte
- Schmuckdesign mit Dreiecksformen
Formeln zur dreieckigen Doppelpyramide
Mantelhöhe (s)
Schräge Höhe der Dreiecks-Seitenflächen mit cot(60°) = 1/√3
Kantenlänge (e)
Länge der Seitenkanten zur Spitze
Gesamthöhe (i)
Doppelte Höhe einer Pyramidenhälfte
Eine Seitenfläche (As)
Fläche eines dreieckigen Seitensegments
Oberfläche (S)
Gesamte Oberfläche aller 6 Dreiecke
Umfang (P)
Umfang der dreieckigen Grundfläche
Volumen (V)
Gesamtvolumen beider Pyramidenhälften mit tan(60°) = √3
Berechnungsbeispiel für eine dreieckige Doppelpyramide
Gegeben
Gesucht: Alle Eigenschaften der dreieckigen Doppelpyramide
1. Mantelhöhe-Berechnung
Für gleichseitiges Dreieck (60°):
\[s = \sqrt{h^2 + \frac{a^2 \cdot \cot^2(\frac{\pi}{3})}{4}}\] \[s = \sqrt{10^2 + \frac{8^2 \cdot (\frac{1}{\sqrt{3}})^2}{4}}\] \[s = \sqrt{100 + \frac{64}{12}} = \sqrt{100 + 5.33} \approx 10.26\]Die Mantelhöhe beträgt etwa 10.26 Längeneinheiten
2. Kantenlänge-Berechnung
Mit s ≈ 10.26:
\[e = \sqrt{s^2 + \left(\frac{a}{2}\right)^2}\] \[e = \sqrt{10.26^2 + 16}\] \[e = \sqrt{105.26+16} \approx 11.01\]Die Kantenlänge beträgt etwa 6.51 Längeneinheiten
3. Volumen-Berechnung
Für a = 8, h = 10:
\[V = \frac{a^2 \cdot h \cdot \sqrt{3}}{6}\] \[V = \frac{8^2 \cdot 10 \cdot \sqrt{3}}{6}\] \[V = \frac{640 \cdot 1.732}{6} \approx 184.6\]Das Volumen beträgt etwa 184.6 Volumeneinheiten
4. Oberfläche-Berechnung
Mit a = 8, s ≈ 10.26:
\[S = 3 \cdot a \cdot s\] \[S = 3 \cdot 8 \cdot 10.26\] \[S \approx 246.24\]Die Oberfläche beträgt etwa 246.24 Flächeneinheiten
5. Vollständige dreieckige Doppelpyramide
Die dreieckige Doppelpyramide mit perfekter symmetrischer Struktur
Die dreieckige Doppelpyramide: Dreieckige Perfektion
Die dreieckige Doppelpyramide ist eine besonders elegante geometrische Struktur, die durch die Verbindung zweier kongruenter Pyramiden an ihrer gemeinsamen gleichseitigen Dreiecksbasis entsteht. Diese elegante Konstruktion führt zu einem perfekt symmetrischen Körper mit 6 kongruenten dreieckigen Seitenflächen, der sowohl mathematische Schönheit als auch praktische Anwendbarkeit verkörpert. Die trigonometrischen Formeln mit der speziellen 60°-Winkel (π/3) und √3-Faktoren zeigen die einzigartige Geometrie des gleichseitigen Dreiecks.
Die Geometrie der dreieckigen Symmetrie
Die dreieckige Doppelpyramide demonstriert die Perfektion der dreieckigen Doppelsymmetrie:
- Deltaeder: Alle 6 Flächen sind kongruente Dreiecke
- C3v-Symmetrie: Dreizählige Rotationssymmetrie mit Spiegelebenen
- Uniformität: Alle Seitenflächen sind kongruent
- Dreiecksbasis: Speziell für gleichseitige Dreiecke optimiert
- Konvexität: Alle Kanten und Ecken zeigen nach außen
- Stabilität: Optimale strukturelle Eigenschaften
- Eleganz: Ideal für dreieckige Konstruktionen
Mathematische Eleganz
√3 Trigonometrische Perfektion
Die Formeln der dreieckigen Doppelpyramide nutzen die √3-Faktoren für gleichseitige Dreiecke mit 60°-Winkeln.
Dreieck-Spezialisierung
Als spezialisierte Form für Dreiecke zeigt sie die einzigartigen Eigenschaften der 3-fachen Symmetrie.
Strukturelle Eleganz
Die perfekte dreieckige Symmetrie macht die Doppelpyramide zu einer bevorzugten Form in Natur und Technik.
Ästhetische Harmonie
Die harmonische Vereinigung zweier Pyramiden mit dreieckiger Basis erzeugt eine einzigartige visuelle Balance.
Zusammenfassung
Die dreieckige Doppelpyramide verkörpert die perfekte Balance zwischen mathematischer Eleganz und dreieckiger Symmetrie. Ihre Struktur aus 6 kongruenten Dreiecken, beschrieben durch elegante √3-Formeln, macht sie zu einem faszinierenden Studienobjekt für Mathematiker, Architekten und Designer. Die Spezialisierung auf gleichseitige Dreiecke mit ihren 60°-Winkeln zeigt die einzigartige Schönheit der 3-fachen Symmetrie. Von der reinen Mathematik bis zur praktischen Anwendung bleibt die dreieckige Doppelpyramide ein faszinierendes Beispiel für die Kraft der dreieckigen Geometrie und die Schönheit der mathematischen Präzision in der dreidimensionalen Welt.
|
|
|
|