Dreieckspyramide Rechner
Rechner und Formeln zur Berechnung einer regelmäßigen Dreieckspyramide
Dreieckspyramide Rechner
Die Regelmäßige Dreieckspyramide
Die regelmäßige Dreieckspyramide ist ein Tetraeder mit einer gleichseitigen dreieckigen Grundfläche und drei gleichschenkligen Seitenflächen.
Tetraeder Eigenschaften
Das einfachste Polyeder: Vier dreieckige Flächen in perfekter Harmonie
Pyramide Struktur
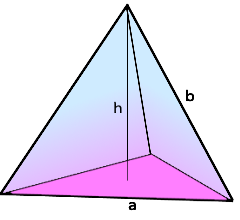
Der Tetraeder mit gleichseitiger Basis.
Platonischer Körper der Perfektion.
|
|
Was ist eine regelmäßige Dreieckspyramide?
Die regelmäßige Dreieckspyramide ist ein faszinierender geometrischer Körper:
- Definition: Pyramide mit gleichseitiger dreieckiger Grundfläche
- Tetraeder: Spezialfall des platonischen Tetraeders
- Flächen: 1 gleichseitige Basis + 3 gleichschenklige Dreiecke
- Ecken: 4 Ecken insgesamt
- Kanten: 6 Kanten (3 Basis + 3 Seiten)
- Symmetrie: Dreizählige Rotationssymmetrie
Geometrische Eigenschaften der Dreieckspyramide
Die regelmäßige Dreieckspyramide zeigt bemerkenswerte geometrische Eigenschaften:
Grundparameter
- Flächen: 4 Dreiecke (1 gleichseitig, 3 gleichschenklig)
- Ecken: 4 Ecken (3 Basis, 1 Spitze)
- Kanten: 6 Kanten (3 Basis, 3 Seiten)
- Euler-Charakteristik: V - E + F = 4 - 6 + 4 = 2
Besondere Eigenschaften
- Tetraeder: Einfachster platonischer Körper
- Gleichseitige Basis: Perfekt symmetrische Grundfläche
- Regelmäßig: Alle Seitenflächen sind gleichschenklig
- Konvex: Keine einspringenden Kanten oder Ecken
Mathematische Beziehungen
Die regelmäßige Dreieckspyramide folgt eleganten mathematischen Gesetzen:
Volumen-Formel
Enthält die Quadratwurzel von 3 für die dreieckige Basis.
Oberflächen-Formel
Kombination aus gleichseitiger Basis und drei gleichschenkligen Dreiecken.
Anwendungen der Dreieckspyramide
Dreieckspyramiden finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Pyramidale Dächer
- Dekorative Spitzen
- Strukturelle Verstrebungen
- Moderne Architektur
Wissenschaft & Technik
- Kristallographische Strukturen
- Molekulare Geometrie
- Optische Prismen
- Mechanische Komponenten
Bildung & Lehre
- Geometrie-Unterricht
- 3D-Geometrie-Studien
- Platonische Körper
- Polyeder-Klassifikation
Kunst & Design
- Geometrische Skulpturen
- Moderne Kunstwerke
- Dekorative Objekte
- Schmuckdesign
Formeln zur regelmäßigen Dreieckspyramide
Kantenlänge (b)
Seitenkante von der Basis zur Spitze
Mantelhöhe (s)
Höhe der Seitenflächen zur Mitte der Basiskante
Grundfläche (A)
Fläche des gleichseitigen Dreiecks
Mantelfläche (Am)
Drei gleichschenklige Dreiecksflächen
Oberfläche (S)
Grundfläche plus Mantelfläche
Volumen (V)
Ein Drittel der Grundfläche mal Höhe
Höhe aus Volumen (h)
Rückrechnung der Höhe aus Volumen und Basislänge
Berechnungsbeispiel für eine regelmäßige Dreieckspyramide
Gegeben
Gesucht: Alle Eigenschaften der regelmäßigen Dreieckspyramide
1. Kantenlänge-Berechnung
Für a = 8, h = 10:
\[b = \sqrt{10^2 + \frac{8^2}{3}}\] \[b = \sqrt{100 + \frac{64}{3}}\] \[b = \sqrt{100 + 21.33} ≈ 11.01\]Die Kantenlänge beträgt etwa 11.01 Längeneinheiten
2. Mantelhöhe-Berechnung
Für b ≈ 11.01, a = 8:
\[s = \sqrt{\frac{4 \cdot 11.01^2 - 8^2}{4}}\] \[s = \sqrt{\frac{484.44 - 64}{4}}\] \[s ≈ \sqrt{105.11} ≈ 10.25\]Die Mantelhöhe beträgt etwa 10.25 Längeneinheiten
3. Grundfläche-Berechnung
Für a = 8:
\[A = \frac{\sqrt{3} \cdot 8^2}{4}\] \[A = \frac{\sqrt{3} \cdot 64}{4}\] \[A ≈ \frac{1.732 \cdot 64}{4} ≈ 27.71\]Die Grundfläche beträgt etwa 27.71 Flächeneinheiten
4. Mantelfläche-Berechnung
Für a = 8, s ≈ 10.25:
\[A_m = \frac{3 \cdot 8 \cdot 10.25}{2}\] \[A_m = \frac{246}{2}\] \[A_m = 123\]Die Mantelfläche beträgt etwa 123 Flächeneinheiten
5. Oberfläche-Berechnung
A ≈ 27.71, Am ≈ 123:
\[S = A + A_m\] \[S = 27.71 + 123\] \[S ≈ 150.71\]Die Oberfläche beträgt etwa 150.71 Flächeneinheiten
6. Volumen-Berechnung
Für a = 8, h = 10:
\[V = \frac{\sqrt{3} \cdot 8^2 \cdot 10}{12}\] \[V = \frac{\sqrt{3} \cdot 64 \cdot 10}{12}\] \[V ≈ \frac{1.732 \cdot 640}{12} ≈ 92.37\]Das Volumen beträgt etwa 92.37 Volumeneinheiten
Zusammenfassung der Ergebnisse
Die regelmäßige Dreieckspyramide mit perfekter geometrischer Harmonie
Die regelmäßige Dreieckspyramide: Der perfekte Tetraeder
Die regelmäßige Dreieckspyramide ist ein faszinierender geometrischer Körper, der die Essenz der dreidimensionalen Geometrie verkörpert. Als einfachster aller Polyeder mit nur vier Flächen repräsentiert sie die grundlegendste Form räumlicher Struktur. Ihre mathematische Schönheit liegt in der perfekten Balance zwischen der gleichseitigen dreieckigen Basis und den drei gleichschenkligen Seitenflächen, die zusammen einen harmonischen und stabilen Körper bilden. Die eleganten Beziehungen mit der Quadratwurzel von 3 durchziehen alle geometrischen Eigenschaften.
Die Geometrie der Einfachheit
Die regelmäßige Dreieckspyramide zeigt die Perfektion geometrischer Einfachheit:
- Tetraeder: Der einfachste aller platonischen Körper
- Dreizählige Symmetrie: Perfekte Rotationssymmetrie um die Höhenachse
- Gleichseitige Basis: Fundament aus einem gleichseitigen Dreieck
- Gleichschenklige Seiten: Drei identische Seitenflächen
- Konvexität: Alle Ecken ragen nach außen
- Stabilität: Optimale strukturelle Eigenschaften
- Universalität: Grundform für komplexere Strukturen
Mathematische Eleganz
Quadratwurzel-Beziehungen
Die Formeln der Dreieckspyramide basieren auf eleganten Quadratwurzel-Beziehungen, insbesondere √3 für die dreieckigen Flächen.
Platonische Perfektion
Als einer der fünf platonischen Körper verkörpert sie mathematische Vollkommenheit und geometrische Harmonie.
Strukturelle Einfachheit
Mit nur vier Flächen ist sie der einfachste dreidimensionale Körper und dennoch von faszinierender Komplexität.
Geometrische Grundlage
Die Dreieckspyramide bildet das Fundament für das Verständnis komplexerer polyedrischer Strukturen.
Zusammenfassung
Die regelmäßige Dreieckspyramide steht als Monument geometrischer Einfachheit und mathematischer Perfektion. Ihre Struktur aus vier dreieckigen Flächen, beschrieben durch elegante Formeln mit Quadratwurzeln, macht sie zu einem fundamentalen Studienobjekt der Geometrie. Von der antiken Mathematik bis zur modernen Architektur bleibt sie ein faszinierendes Beispiel dafür, wie einfachste Formen die komplexesten Wahrheiten über Raum, Struktur und Symmetrie offenbaren können. Als Tetraeder verkörpert sie die Essenz dreidimensionaler Existenz und zeigt, dass wahre geometrische Schönheit oft in der größten Einfachheit liegt.
|
|
|
|