Zylinderabschnitt Rechner
Rechner und Formeln zur Berechnung eines schrägen Zylinderabschnitts
Zylinderabschnitt Rechner
Der Zylinderabschnitt
Der Zylinderabschnitt ist ein schräg abgeschnittener Zylinder mit unterschiedlichen Höhen.
Zylinderabschnitt Eigenschaften
Der Zylinderabschnitt: Schräg abgeschnittener Zylinder mit elliptischer Schnittfläche
Zylinderabschnitt Visualisierung
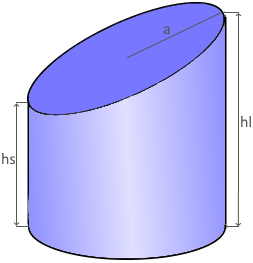
Zylinderabschnitt
Schräg abgeschnittener Zylinder
Parameter
r: Radius der Grundfläche
hs: Kurze Höhe (Minimum)
hl: Lange Höhe (Maximum)
a: Große Halbachse der Ellipse
Schräg abgeschnittener Zylinder.
Elliptische Schnittflächen.
|
|
Was ist ein Zylinderabschnitt?
Der Zylinderabschnitt ist ein faszinierender geometrischer Körper:
- Definition: Durch schrägen Schnitt entstandener Zylinderteil
- Charakteristika: Zwei unterschiedliche Höhen hs und hl
- Eigenschaften: Elliptische Ober- und Unterflächen
- Schnittwinkel: Bestimmt die Ellipsenform der Schnittflächen
- Anwendung: Rohrleitungen, Architektur, Maschinenbau
- Mathematik: Kombination aus Zylinder- und Ellipsengeometrie
Geometrische Eigenschaften des Zylinderabschnitts
Der Zylinderabschnitt zeigt charakteristische geometrische Eigenschaften:
Grundparameter
- Radius r: Radius der kreisförmigen Grundfläche
- Kurze Höhe hs: Minimale Höhe des Abschnitts
- Lange Höhe hl: Maximale Höhe des Abschnitts
- Mittlere Höhe: hm = (hs + hl)/2
Besondere Eigenschaften
- Elliptische Schnittflächen: Durch schrägen Schnitt entstanden
- Trapezförmiger Mantel: Seitenfläche als Trapez abwickelbar
- Halbachse der Ellipse: a = √(r² + ((hl-hs)/2)²)
- Volumenerhaltung: Mittlere Höhe bestimmt das Volumen
Mathematische Beziehungen des Zylinderabschnitts
Der Zylinderabschnitt folgt eleganten mathematischen Gesetzen:
Volumen-Formel
Das Volumen wird durch die mittlere Höhe bestimmt. Elegante Mittelwertbildung.
Ellipsen-Halbachse
Die große Halbachse der elliptischen Schnittflächen durch Pythagoras.
Anwendungen des Zylinderabschnitts
Zylinderabschnitte finden Anwendung in verschiedenen Bereichen:
Rohrleitungstechnik
- Schräge Rohrleitungsverbindungen
- Übergangsstücke zwischen Leitungen
- Rohrabzweigungen
- Flanschverbindungen
Architektur & Bauwesen
- Dachkonstruktionen
- Schräge Säulenverbindungen
- Treppengeländer
- Architektonische Details
Maschinenbau & Automotive
- Getriebewellen
- Kupplungselemente
- Auspuffanlagen
- Hydraulikkomponenten
Verfahrenstechnik
- Schräge Behälteröffnungen
- Trichterelemente
- Dosiereinrichtungen
- Förderanlagen
Formeln zum Zylinderabschnitt
Volumen (V)
Volumen durch mittlere Höhe
Basisfläche (A)
Kreisförmige Grundfläche
Seitenfläche (L)
Trapezförmige Mantelfläche
Halbachse (a)
Große Halbachse der Ellipse
Gesamtoberfläche (S)
Mantelfläche plus elliptische Grund- und Deckfläche
Weitere Parameter
\[P = 2\pi r\]
\[h_m = \frac{h_s + h_l}{2}\]
\[\Delta h = h_l - h_s\]
\[\tan \alpha = \frac{\Delta h}{2r}\]
Der Zylinderabschnitt kombiniert Zylinder- und Ellipsengeometrie
Berechnungsbeispiel für einen Zylinderabschnitt
Gegeben
Gesucht: Alle Parameter des Zylinderabschnitts
1. Mittlere Höhe und Volumen
Für r = 5 cm, hs = 4 cm, hl = 6 cm:
\[h_m = \frac{h_s + h_l}{2} = \frac{4 + 6}{2} = 5 \text{ cm}\] \[V = \pi r^2 h_m = \pi \cdot 25 \cdot 5 = 125\pi\] \[V ≈ 392.70 \text{ cm}^3\]Das Volumen beträgt etwa 392.70 cm³
2. Ellipsen-Halbachse
Große Halbachse der Schnittellipse:
\[\frac{h_l - h_s}{2} = \frac{6 - 4}{2} = 1 \text{ cm}\] \[a = \sqrt{r^2 + 1^2} = \sqrt{25 + 1}\] \[a = \sqrt{26} ≈ 5.10 \text{ cm}\]Die Ellipsen-Halbachse beträgt etwa 5.10 cm
3. Grundflächen-Berechnung
Basisfläche und Umfang:
\[A = \pi r^2 = \pi \cdot 25 ≈ 78.54 \text{ cm}^2\] \[P = 2\pi r = 10\pi ≈ 31.42 \text{ cm}\]Basisfläche ≈ 78.54 cm², Umfang ≈ 31.42 cm
4. Mantelflächen-Berechnung
Trapezförmige Seitenfläche:
\[L = \pi r (h_s + h_l)\] \[L = \pi \cdot 5 \cdot (4 + 6)\] \[L = 50\pi ≈ 157.08 \text{ cm}^2\]Die Mantelfläche beträgt etwa 157.08 cm²
5. Gesamtoberfläche
Komplette Oberflächenberechnung:
\[S = L + \pi r (r + a)\] \[S = 157.08 + \pi \cdot 5 \cdot (5 + 5.10)\] \[S = 157.08 + 15.7\pi \cdot 10.10\] \[S ≈ 157.08 + 497.87 ≈ 654.95 \text{ cm}^2\]Die Gesamtoberfläche beträgt etwa 654.95 cm²
6. Geometrische Analyse
tan(α) = Δh/(2r) = 2/10 = 0.2
α ≈ 11.31°
a/r = 5.10/5 ≈ 1.02
Schwach elliptisch
hl/hs = 6/4 = 1.5
50% Höhenunterschied
Der Zylinderabschnitt zeigt moderaten schrägen Schnitt
7. Zusammenfassung
Der Zylinderabschnitt mit allen charakteristischen Parametern
8. Praktisches Beispiel: Rohrabzweigung
V ≈ 392.70 cm³
≈ 0.39 Liter
S ≈ 654.95 cm²
Blechverbrauch
Sanfter Übergang
α = 11.31° Neigung
Eine Rohrabzweigung mit optimaler Strömungsführung und minimalem Druckverlust
9. Vergleich mit normalem Zylinder
r=5, hs=4, hl=6
V≈392.70 cm³
r=5, h=5
V≈392.70 cm³
Gleiches Volumen!
Mittlere Höhe entscheidet
Das Volumen wird nur durch die mittlere Höhe bestimmt - elegante Geometrie!
Der Zylinderabschnitt: Eleganz der Schnittgeometrie
Der Zylinderabschnitt ist ein faszinierender geometrischer Körper, der die Eleganz der klassischen Zylindergeometrie mit der Komplexität elliptischer Schnittflächen verbindet. Als durch schrägen Schnitt entstandener Zylinderteil vereint er in sich die Praktikabilität zylindrischer Formen mit der mathematischen Raffinesse elliptischer Geometrie. Diese einzigartige Kombination macht ihn zu einem unverzichtbaren Element in Rohrleitungstechnik, Architektur und Maschinenbau, wo präzise Übergänge und optimale Strömungsführung entscheidend sind.
Die Geometrie des schrägen Schnitts
Der Zylinderabschnitt zeigt die Perfektion kontrollierter Schnittgeometrie:
- Zwei charakteristische Höhen: hs (kurz) und hl (lang) definieren die Form
- Mittlere Höhe hm = (hs+hl)/2: Bestimmt das Volumen elegant
- Elliptische Schnittflächen: Durch schrägen Schnitt entstehende Ellipsen
- Trapezförmiger Mantel: Abwickelbar zu einem perfekten Trapez
- Halbachsen-Beziehung: a = √(r² + ((hl-hs)/2)²) nach Pythagoras
- Neigungswinkel α: tan(α) = (hl-hs)/(2r) für Strömungsoptimierung
- Volumenerhaltung: Nur die mittlere Höhe bestimmt das Volumen
Vielseitige Anwendungen
Rohrleitungstechnik
Schräge Rohrabschnitte ermöglichen sanfte Übergänge zwischen verschiedenen Leitungsebenen und optimieren Strömungsverhalten bei minimalen Druckverlusten.
Architektonische Eleganz
In der Architektur schaffen Zylinderabschnitte fließende Übergänge zwischen verschiedenen Gebäudebereichen und ermöglichen innovative Dachkonstruktionen.
Maschinenbau-Präzision
Präzise gefertigte Zylinderabschnitte in Getrieben und Kupplungen gewährleisten optimale Kraftübertragung bei kompakter Bauweise.
Verfahrenstechnische Effizienz
Schräge Behälteröffnungen und Trichterelemente nutzen die Schwerkraft optimal und verbessern Entleerung und Dosierung erheblich.
Zusammenfassung
Der Zylinderabschnitt verkörpert die perfekte Synthese aus geometrischer Präzision und praktischer Funktionalität. Seine durch schrägen Schnitt charakterisierte Form, beschrieben durch die elegante Volumenformel V = πr²(hs+hl)/2, zeigt, wie die mittlere Höhe das gesamte Volumen bestimmt - ein Triumph der mathematischen Eleganz. Die elliptischen Schnittflächen mit ihrer Halbachsen-Beziehung a = √(r² + ((hl-hs)/2)²) demonstrieren die perfekte Anwendung des Pythagoras'schen Lehrsatzes in der praktischen Geometrie. Von optimierten Rohrleitungsverbindungen über elegante Architekturelemente bis hin zu präzisen Maschinenbaukomponenten - der Zylinderabschnitt beweist, dass die schönsten geometrischen Lösungen oft aus der Kombination einfacher Prinzipien entstehen. Er ist der lebende Beweis dafür, dass kontrollierte Asymmetrie zu perfekter Funktionalität führt und zeigt, wie Schnittgeometrie praktische Probleme elegant und effizient löst.
|
|
|
|