Truncated Square Pyramid Calculator
Calculator and formulas for truncated square pyramid (frustum) volume and surface area
Square Frustum Calculator
The Truncated Square Pyramid
A truncated square pyramid is a frustum with square bases of different sizes connected by trapezoidal faces.
Square Frustum Properties
Geometric shape: A square pyramid with the top cut off parallel to the base
Square Frustum Structure
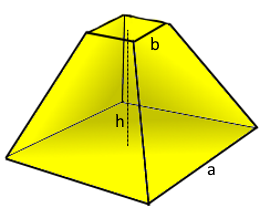
Square pyramid with parallel top cut.
Perfect square frustum geometry.
|
|
What is a truncated square pyramid?
A truncated square pyramid (square frustum) is an elegant geometric shape:
- Definition: A square pyramid with the top cut off parallel to the base
- Shape: Two parallel square bases of different sizes
- Faces: 2 square bases + 4 identical trapezoidal lateral faces
- Vertices: 8 vertices total
- Edges: 12 edges (4+4+4)
- Symmetry: 4-fold rotational symmetry
Geometric Properties of the Square Frustum
The truncated square pyramid exhibits exceptional geometric properties:
Basic Parameters
- Faces: 6 faces total (2 squares + 4 trapezoids)
- Vertices: 8 vertices (4 on top, 4 on bottom)
- Edges: 12 edges (4 top, 4 bottom, 4 vertical)
- Euler characteristic: V - E + F = 8 - 12 + 6 = 2
Special Properties
- Square symmetry: Perfect 4-fold rotational symmetry
- Uniform tapering: All four sides taper equally
- Identical trapezoids: All lateral faces are congruent
- Convex: All vertices point outward
Mathematical Relationships
The truncated square pyramid follows elegant mathematical laws:
Volume Formula
Combines squares and cross product. Simple and elegant formula.
Surface Area Formula
Two squares plus trapezoidal faces. Includes slant height calculation.
Applications of the Square Frustum
Truncated square pyramids find applications in various fields:
Architecture & Construction
- Building foundations and footings
- Decorative architectural elements
- Monument and statue bases
- Garden planters and landscaping
Engineering & Manufacturing
- Industrial hoppers and containers
- Conveyor system components
- Mechanical fasteners and brackets
- Structural supports and connectors
Science & Technology
- Optical prisms and lens components
- Crystal growth and materials science
- Antenna design and engineering
- Fluid dynamics and flow studies
Art & Design
- Sculptural elements and installations
- Furniture design and accessories
- Decorative objects and vases
- Architectural model making
Truncated Square Pyramid Formulas
Volume (V)
Elegant formula with quadratic and cross terms
Lateral Area (A)
Four identical trapezoidal faces with slant height
Surface Area (S)
Lateral area plus top and bottom square areas
Height (h)
Height derived from volume formula
Slant Height and Base Areas
\(s = \sqrt{\left(\frac{a-b}{2}\right)^2 + h^2}\)
\(A_b = a^2\)
\(A_t = b^2\)
Essential measurements for the square frustum
Calculation Example for a Truncated Square Pyramid
Given
Find: Volume, surface area, and all components of the square frustum
1. Volume Calculation
Using the volume formula:
\[V = \frac{6}{3}(8^2 + 8 \cdot 5 + 5^2)\] \[V = 2(64 + 40 + 25)\] \[V = 2 \cdot 129 = 258\]The volume is exactly 258 cubic units
2. Base Areas Calculation
Square areas:
\[A_b = a^2 = 8^2 = 64\] \[A_t = b^2 = 5^2 = 25\]Total base area: 64 + 25 = 89
Base area: 64 sq units, Top area: 25 sq units
3. Slant Height Calculation
Slant height for trapezoidal faces:
\[s = \sqrt{\left(\frac{8-5}{2}\right)^2 + 6^2}\] \[s = \sqrt{1.5^2 + 6^2} = \sqrt{2.25 + 36}\] \[s = \sqrt{38.25} ≈ 6.18\]The slant height is approximately 6.18 units
4. Surface Area Calculation
Lateral area:
\[A = 2(8+5) \cdot 6.18 = 2 \cdot 13 \cdot 6.18\] \[A ≈ 160.68\]Total surface area:
\[S = 160.68 + 64 + 25 = 249.68\]Total surface area is approximately 249.68 square units
Complete Results Summary
Perfect square frustum with symmetric trapezoidal lateral faces
The Truncated Square Pyramid: Symmetric Geometric Excellence
The truncated square pyramid, also known as a square frustum, represents the pinnacle of geometric symmetry and practical utility. This remarkable shape emerges when a square pyramid is cut by a plane parallel to its base, creating two parallel square faces connected by four identical trapezoidal lateral faces. The mathematical beauty of this form lies in its perfect 4-fold rotational symmetry and the elegant simplicity of its formulas, which combine quadratic terms with cross products to describe its volume and surface properties with remarkable precision.
The Geometry of Perfect Symmetry
The truncated square pyramid showcases the epitome of symmetric design:
- Square bases: Two parallel squares providing perfect stability
- Identical trapezoids: Four congruent lateral faces ensuring uniformity
- 4-fold symmetry: Perfect rotational symmetry around the central axis
- Uniform tapering: Equal reduction in all four directions
- Structural efficiency: Optimal load distribution and material usage
- Manufacturing simplicity: Easy to construct with standard tools
- Aesthetic appeal: Pleasing proportions in all applications
Mathematical Elegance
Quadratic Volume Formula
The volume formula elegantly combines the squares of both bases with their cross product, creating a perfect mathematical representation of the gradual transition.
Symmetric Surface Calculation
The surface area combines two simple square areas with the lateral area of four identical trapezoids, all calculated using a single slant height.
Pythagorean Relationships
The slant height calculation involves the Pythagorean theorem, connecting the vertical height with the horizontal taper dimensions.
Engineering Precision
The formulas translate directly to practical engineering calculations for material quantities, structural loads, and manufacturing specifications.
Summary
The truncated square pyramid stands as a masterpiece of geometric perfection, combining mathematical elegance with practical utility. Its simple yet powerful formulas—featuring quadratic terms and cross products—accurately describe a shape that appears throughout human civilization, from ancient monuments to modern industrial applications. The perfect 4-fold symmetry ensures uniform properties in all directions, making it ideal for structural applications where stability and predictability are paramount. Whether serving as the foundation of a building, the hopper of an industrial system, or the base of a decorative element, the square frustum provides optimal solutions through its harmonious blend of geometric beauty and functional efficiency. Understanding its mathematical relationships enables engineers, architects, and designers to harness this shape's full potential in creating structures that are both aesthetically pleasing and structurally sound.