Quadratischer Pyramidenstumpf Rechner
Rechner und Formeln zur Berechnung eines quadratischen Pyramidenstumpf
Pyramidenstumpf Rechner
Der Pyramidenstumpf (Frustum)
Diese Funktion berechnet das Volumen und die Oberfläche eines quadratischen Pyramidenstumpf. Zur Berechnung geben Sie die Höhe, Basisseite und Deckseite ein.
Pyramidenstumpf Eigenschaften
Der abgeschnittene Pyramid: Entstanden durch horizontalen Schnitt durch eine Pyramide
Pyramidenstumpf Struktur
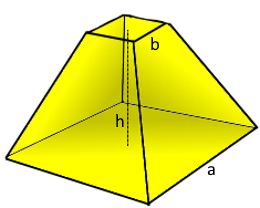
Der quadratische Pyramidenstumpf (Frustum).
Entstanden durch Abschneiden einer Pyramide.
|
|
Was ist ein quadratischer Pyramidenstumpf?
Der quadratische Pyramidenstumpf (auch Frustum genannt) ist eine praktische geometrische Form:
- Definition: Entsteht durch horizontalen Schnitt durch eine quadratische Pyramide
- Struktur: Zwei parallele quadratische Flächen unterschiedlicher Größe
- Flächen: 2 Quadrate (Basis + Deckfläche) + 4 Trapeze (Seitenflächen)
- Ecken: 8 Ecken (4 unten + 4 oben)
- Kanten: 12 Kanten (4 unten + 4 oben + 4 seitlich)
- Anwendung: Praktisch in Architektur und Technik
Geometrische Eigenschaften des Pyramidenstumpfs
Der quadratische Pyramidenstumpf zeigt interessante geometrische Eigenschaften:
Grundparameter
- Flächen: 6 (2 Quadrate + 4 Trapeze)
- Ecken: 8 (4 unten + 4 oben)
- Kanten: 12 (4+4+4)
- Euler-Charakteristik: V - E + F = 8 - 12 + 6 = 2
Besondere Eigenschaften
- Praktikabilität: Sehr praktische Form
- Stabilität: Gute strukturelle Eigenschaften
- Ähnlichkeit: Basis und Deckfläche sind ähnlich
- Skalierung: Entstehen durch proportionale Verkleinerung
Mathematische Beziehungen
Der quadratische Pyramidenstumpf folgt eleganten mathematischen Gesetzen:
Volumen-Formel
Kombination aus beiden Quadraten. Elegant und praktisch.
Mantelflächen-Formel
Vier trapezförmige Seitenflächen. Pythagoras für Schräghöhe.
Anwendungen des Pyramidenstumpfs
Quadratische Pyramidenstümpfe finden Anwendung in verschiedenen Bereichen:
Architektur & Bauwesen
- Fundamente und Sockel
- Stützmauern und Böschungen
- Dekorative Bauelemente
- Treppenabsätze
Technik & Industrie
- Behälter und Trichter
- Maschinenbauteile
- Gießformen
- Förderanlagen
Bildung & Lehre
- Geometrie-Unterricht
- Volumenberechnungen
- 3D-Geometrie-Studien
- Praktische Mathematik
Kunst & Design
- Skulpturen und Installationen
- Möbeldesign
- Landschaftsgestaltung
- Produktdesign
Formeln zum quadratischen Pyramidenstumpf
Volumen (V)
Volumen als Summe der quadratischen Terme
Mantelfläche (A)
Vier trapezförmige Seitenflächen mit Schräghöhe
Oberfläche (S)
Mantelfläche plus beide quadratische Flächen
Höhe (h)
Höhe aus Volumen und quadratischen Termen
Zusätzliche Parameter
\(s = \sqrt{\left(\frac{a-b}{2}\right)^2 + h^2}\)
\(P_a = 4a\)
\(P_b = 4b\)
\(A_T = \frac{(a+b) \cdot s}{2}\)
Alle Parameter folgen aus der Frustum-Geometrie
Berechnungsbeispiel für einen quadratischen Pyramidenstumpf
Gegeben
Gesucht: Alle Eigenschaften des quadratischen Pyramidenstumpfs
1. Volumen-Berechnung
Für a=5, b=4, h=3:
\[V = \frac{(a^2 + ab + b^2) \cdot h}{3}\] \[V = \frac{(5^2 + 5 \cdot 4 + 4^2) \cdot 3}{3}\] \[V = \frac{(25 + 20 + 16) \cdot 3}{3}\] \[V = \frac{61 \cdot 3}{3} = 61\]Das Volumen beträgt 61 Volumeneinheiten
2. Schräghöhe-Berechnung
Schräghöhe der Trapeze:
\[s = \sqrt{\left(\frac{a-b}{2}\right)^2 + h^2}\] \[s = \sqrt{\left(\frac{5-4}{2}\right)^2 + 3^2}\] \[s = \sqrt{0.5^2 + 9} = \sqrt{0.25 + 9}\] \[s = \sqrt{9.25} ≈ 3.04\]Die Schräghöhe beträgt etwa 3.04 Längeneinheiten
3. Mantelflächen-Berechnung
Vier trapezförmige Seitenflächen:
\[A = 2(a+b) \cdot s\] \[A = 2(5+4) \cdot 3.04\] \[A = 2 \cdot 9 \cdot 3.04\] \[A = 18 \cdot 3.04 ≈ 54.72\]Die Mantelfläche beträgt etwa 54.72 Flächeneinheiten
4. Oberflächen-Berechnung
Mantelfläche + beide Quadrate:
\[S = A + a^2 + b^2\] \[S = 54.72 + 5^2 + 4^2\] \[S = 54.72 + 25 + 16\] \[S = 54.72 + 41 = 95.72\]Die Oberfläche beträgt etwa 95.72 Flächeneinheiten
5. Zusätzliche Parameter
Weitere interessante Werte:
Basis-Umfang: \(P_a = 4 \cdot 5 = 20\)Deck-Umfang: \(P_b = 4 \cdot 4 = 16\)
Eine Trapez-Fläche: \(\frac{54.72}{4} ≈ 13.68\)
Basis-Umfang: 20, Deck-Umfang: 16, Trapez-Fläche: 13.68
6. Der perfekte Pyramidenstumpf
Der quadratische Pyramidenstumpf mit praktischen Proportionen
Der quadratische Pyramidenstumpf: Praktische Geometrie
Der quadratische Pyramidenstumpf (Frustum) ist eine der praktischsten geometrischen Formen überhaupt. Entstanden durch das horizontale Abschneiden einer quadratischen Pyramide, verbindet er die Stabilität der Pyramide mit der Funktionalität einer ebenen Deckfläche. Diese Form findet sich überall in der Architektur, im Maschinenbau und in der Natur. Die mathematischen Beziehungen sind elegant und folgen klaren Prinzipien, die auf der Ähnlichkeit der beiden parallelen Quadrate und den trapezförmigen Verbindungsflächen basieren.
Die Geometrie der Praktikabilität
Der quadratische Pyramidenstumpf zeigt die Perfektion der praktischen Geometrie:
- Duale Basis: Zwei parallele quadratische Flächen für optimale Stabilität
- Trapezförmige Seiten: Vier identische Trapeze verbinden die Quadrate
- Ähnlichkeitsprinzip: Basis und Deckfläche sind geometrisch ähnlich
- Strukturelle Effizienz: Optimales Verhältnis von Stabilität zu Material
- Skalierbarkeit: Proportionen bleiben bei jeder Größe erhalten
- Vielseitigkeit: Adaptierbar für verschiedenste Anwendungen
- Funktionalität: Kombiniert die Vorteile von Pyramide und Quader
Mathematische Eleganz
Volumen-Harmonie
Die Volumenformel V = ⅓h(a² + ab + b²) zeigt die elegante Verbindung der drei quadratischen Terme, die die geometrische Beziehung zwischen den Flächen ausdrückt.
Schräghöhen-Prinzip
Die Mantelfläche basiert auf der Schräghöhe, die durch den Satz des Pythagoras aus der Höhe und der Differenz der Seitenlängen berechnet wird.
Praktische Berechenbarkeit
Alle Formeln sind einfach anwendbar und ermöglichen schnelle Berechnungen für praktische Anwendungen in Technik und Architektur.
Universelle Anwendbarkeit
Die mathematischen Beziehungen gelten unabhängig von der Größe und ermöglichen die Anwendung in verschiedensten Maßstäben.
Zusammenfassung
Der quadratische Pyramidenstumpf ist ein Paradebeispiel für praktische Geometrie. Seine Entstehung durch das Abschneiden einer Pyramide führt zu einer Form, die die Stabilität der ursprünglichen Pyramide mit der Funktionalität einer ebenen Oberfläche verbindet. Die mathematischen Formeln sind elegant und praxistauglich, basierend auf den Prinzipien der Ähnlichkeit und des Satzes von Pythagoras. Von Fundamenten im Bauwesen über Behälter in der Industrie bis hin zu dekorativen Elementen in der Architektur zeigt der Pyramidenstumpf, wie mathematische Schönheit und praktische Anwendbarkeit Hand in Hand gehen können. Seine Vielseitigkeit und strukturelle Effizienz machen ihn zu einer der wertvollsten Formen in der angewandten Geometrie.
|
|
|
|