Absolute Value (Modulus) of Complex Numbers
Understanding magnitude and distance in the complex plane
Introduction to the Modulus
In the discussion of the complex plane, we learned that every complex number can be represented as a vector from the origin to a point \((a, b)\). The absolute value (also called modulus) of a complex number is simply the length of this vector.
The modulus is always a non-negative real number and provides important information about the "size" or "magnitude" of a complex number.
The absolute value connects the geometric representation of complex numbers (as vectors) with the algebraic representation. It measures the distance from the origin to the point representing the complex number.
Geometric Interpretation
When we represent a complex number \(z = a + bi\) geometrically in the complex plane, we get a right triangle with:
- Horizontal leg: Length \(a\) (real part)
- Vertical leg: Length \(b\) (imaginary part)
- Hypotenuse: The vector from origin to \((a, b)\)
The absolute value corresponds to the length of the hypotenuse. We can find this using the Pythagorean theorem.
Complex Number as Right Triangle:
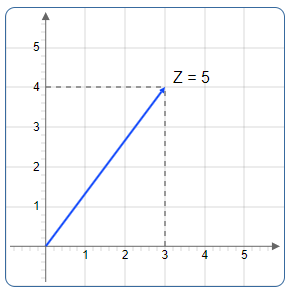
The hypotenuse represents the absolute value \(|z|\)
Definition and Formulas
The absolute value (modulus) of a complex number can be calculated using different but equivalent formulas.
Formula 1: Using the Pythagorean Theorem
For a complex number \(z = a + bi\), the absolute value is:
\(\displaystyle |z| = \sqrt{a^2 + b^2}\)
This formula comes directly from the Pythagorean theorem applied to the right triangle formed by the real and imaginary parts.
Formula 2: Using the Conjugate
There is an elegant alternative formula using the complex conjugate:
\(\displaystyle |z| = \sqrt{z \cdot \overline{z}}\)
where \(\overline{z}\) is the complex conjugate of \(z\).
If \(z = a + bi\), then \(\overline{z} = a - bi\), so:
Therefore: \(\displaystyle |z| = \sqrt{z \cdot \overline{z}} = \sqrt{a^2 + b^2}\)
Calculating the Modulus
Example 1: Simple Complex Number
Calculate \(|3 + 4i|\)
Using Method 1 (Pythagorean):
Using Method 2 (Conjugate):
Result: The absolute value is \(5\).
Example 2: Negative Imaginary Part
Calculate \(|3 - 4i|\)
Important: The absolute values of \(3 + 4i\) and \(3 - 4i\) are the same!
Example 3: Pure Real Number
Calculate \(|5|\)
For a purely real number \(z = 5 = 5 + 0i\):
The absolute value of a real number equals the real number itself (if positive).
Example 4: Pure Imaginary Number
Calculate \(|3i|\)
For a purely imaginary number \(z = 3i = 0 + 3i\):
Properties of the Modulus
Non-negativity
\(\displaystyle |z| \geq 0\)The modulus is always non-negative
\(|z| = 0\) only if \(z = 0\)
Conjugate Property
\(\displaystyle |z| = |\overline{z}| = |-z|\)Modulus of conjugate and negation equals original
Product Property
\(\displaystyle |z_1 \cdot z_2| = |z_1| \cdot |z_2|\)Modulus of product equals product of moduli
Quotient Property
\(\displaystyle \left|\frac{z_1}{z_2}\right| = \frac{|z_1|}{|z_2|}\)Modulus of quotient equals quotient of moduli
Triangle Inequality
\(\displaystyle |z_1 + z_2| \leq |z_1| + |z_2|\)The modulus of a sum is at most the sum of moduli
Power Property
\(\displaystyle |z^n| = |z|^n\)Modulus of a power equals the power of modulus
Modulus Summary
| Complex Number | Modulus Calculation | Result |
|---|---|---|
| \(3 + 4i\) | \(\sqrt{3^2 + 4^2}\) | \(5\) |
| \(1 + i\) | \(\sqrt{1^2 + 1^2}\) | \(\sqrt{2}\) |
| \(5\) | \(\sqrt{5^2 + 0^2}\) | \(5\) |
| \(3i\) | \(\sqrt{0^2 + 3^2}\) | \(3\) |
| \(-2 - 2i\) | \(\sqrt{(-2)^2 + (-2)^2}\) | \(2\sqrt{2}\) |
Key Points to Remember
- The modulus is the distance from the origin to the complex number in the plane
- Formula: \(|z| = \sqrt{a^2 + b^2}\) for \(z = a + bi\)
- The modulus is always a non-negative real number
- Conjugate numbers have the same modulus: \(|z| = |\overline{z}|\)
- Opposite numbers have the same modulus: \(|z| = |-z|\)
- The modulus can be calculated using the conjugate: \(|z| = \sqrt{z \cdot \overline{z}}\)
- Modulus properties are useful for complex number arithmetic
Applications and Tools
The modulus of complex numbers is fundamental in many applications:
- Signal Processing: Represents signal magnitude and amplitude
- Electrical Engineering: Calculates impedance magnitude
- Physics: Represents wave amplitudes and quantum probabilities
- Control Systems: Analyzes system stability
- Geometry: Measures distances in the complex plane
|
|