Converting Polar to Normal Form

Transform complex numbers from polar to rectangular (normal) form

Introduction to Polar-to-Normal Conversion

In the polar form representation of complex numbers, we describe them using a magnitude (distance from origin) and an angle (direction). To perform arithmetic operations or work with the real and imaginary parts directly, we often need to convert this to the normal form (also called rectangular form).

This conversion uses trigonometric functions and is essential for working with complex numbers in practical applications.

Key Insight:

The conversion from polar to normal form extracts the real and imaginary components from the magnitude and angle using basic trigonometry.

Geometric Foundation

When we represent a complex number in the complex plane, the magnitude \(r\) and argument \(\varphi\) define a vector from the origin. This vector forms a right triangle with the real and imaginary axes.

  • Hypotenuse: The vector with length \(r\)
  • Horizontal leg (adjacent): The real part \(a\)
  • Vertical leg (opposite): The imaginary part \(b\)
  • Angle: The argument \(\varphi\) from the positive real axis

Right Triangle in the Complex Plane:

Right triangle showing polar to rectangular conversion

The real part is the adjacent side, imaginary part is the opposite side

Conversion Formula

Using trigonometric ratios from the right triangle, we can extract the real and imaginary parts from the magnitude and angle.

Component Extraction

Conversion Formulas:

Given a complex number in polar form with magnitude \(r\) and argument \(\varphi\):

Real Part (Cosine):
\(\displaystyle a = r \cos(\varphi)\)
Imaginary Part (Sine):
\(\displaystyle b = r \sin(\varphi)\)

Complete Conversion

Full Conversion Formula:

The complex number in normal form is:

Normal Form from Polar:
\(\displaystyle z = r(\cos\varphi + i\sin\varphi) = r\cos\varphi + ir\sin\varphi = a + bi\)
Why This Works:

In the right triangle formed by the complex number:

  • \(\cos\varphi = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{a}{r}\) → \(a = r\cos\varphi\)
  • \(\sin\varphi = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{b}{r}\) → \(b = r\sin\varphi\)

Step-by-Step Conversion Process

1Identify magnitude and argument
Determine \(r\) (magnitude) and \(\varphi\) (argument) from the polar form
2Calculate the real part
Use \(\displaystyle a = r \cos(\varphi)\)
3Calculate the imaginary part
Use \(\displaystyle b = r \sin(\varphi)\)
4Write the normal form
Express as \(z = a + bi\)

Conversion Examples

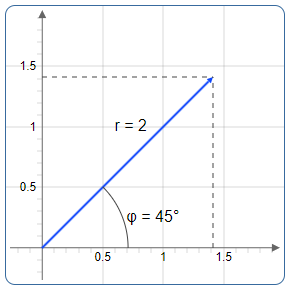
Example 1: 45° Angle (Simple Case)

Convert \(z = 2(\cos 45° + i\sin 45°)\) to normal form

Given: \(r = 2\), \(\varphi = 45°\)

Step 1-2: Calculate real part

\(\displaystyle a = 2 \cos(45°) = 2 \cdot \frac{\sqrt{2}}{2} = \sqrt{2}\)

Step 3: Calculate imaginary part

\(\displaystyle b = 2 \sin(45°) = 2 \cdot \frac{\sqrt{2}}{2} = \sqrt{2}\)

Step 4: Normal form

\(\displaystyle z = \sqrt{2} + i\sqrt{2} \approx 1.414 + 1.414i\)

Example 2: 60° Angle

Convert \(z = 4(\cos 60° + i\sin 60°)\) to normal form

Given: \(r = 4\), \(\varphi = 60°\)

Real part:

\(\displaystyle a = 4 \cos(60°) = 4 \cdot \frac{1}{2} = 2\)

Imaginary part:

\(\displaystyle b = 4 \sin(60°) = 4 \cdot \frac{\sqrt{3}}{2} = 2\sqrt{3}\)

Normal form:

\(\displaystyle z = 2 + 2\sqrt{3}i \approx 2 + 3.464i\)

Example 3: Arbitrary Angle

Convert \(z = 5(\cos 30° + i\sin 30°)\) to normal form

Given: \(r = 5\), \(\varphi = 30°\)

Real part:

\(\displaystyle a = 5 \cos(30°) = 5 \cdot \frac{\sqrt{3}}{2} = \frac{5\sqrt{3}}{2}\)

Imaginary part:

\(\displaystyle b = 5 \sin(30°) = 5 \cdot \frac{1}{2} = \frac{5}{2}\)

Normal form:

\(\displaystyle z = \frac{5\sqrt{3}}{2} + \frac{5}{2}i \approx 4.330 + 2.5i\)

Example 4: Standard Angles

Common conversions
  • \(1(\cos 0° + i\sin 0°) = 1\)
  • \(1(\cos 90° + i\sin 90°) = i\)
  • \(1(\cos 180° + i\sin 180°) = -1\)
  • \(1(\cos 270° + i\sin 270°) = -i\)

Special Cases and Tips

Standard Trigonometric Values

Angle Degrees \(\cos(\varphi)\) \(\sin(\varphi)\)
\(0\) \(0°\) \(1\) \(0\)
\(\frac{\pi}{6}\) \(30°\) \(\frac{\sqrt{3}}{2}\) \(\frac{1}{2}\)
\(\frac{\pi}{4}\) \(45°\) \(\frac{\sqrt{2}}{2}\) \(\frac{\sqrt{2}}{2}\)
\(\frac{\pi}{3}\) \(60°\) \(\frac{1}{2}\) \(\frac{\sqrt{3}}{2}\)
\(\frac{\pi}{2}\) \(90°\) \(0\) \(1\)
Helpful Tip:

Memorizing the standard angle values (0°, 30°, 45°, 60°, 90°) significantly speeds up conversion calculations. For other angles, use a scientific calculator.

Practical Considerations

Calculator Settings
Ensure your calculator is set to the correct angle mode
(degrees or radians as needed)
Verification
After conversion, verify by computing:
\(\displaystyle r = \sqrt{a^2 + b^2}\)
Angle Range
Be aware that angles can be expressed in multiple equivalent forms
(e.g., 270° = -90°)
Complete Circle
Angles repeat every 360° or 2π radians
Use the principal value when specified

Key Points to Remember

  • The real part is calculated using cosine: \(a = r\cos(\varphi)\)
  • The imaginary part is calculated using sine: \(b = r\sin(\varphi)\)
  • The conversion formula is: \(z = r(\cos\varphi + i\sin\varphi) = a + bi\)
  • Standard angles (0°, 30°, 45°, 60°, 90°) produce exact values
  • For other angles, a calculator is needed
  • Always verify the result by checking \(r = \sqrt{a^2 + b^2}\)
  • Angles can be expressed in radians or degrees


























Is this page helpful?            
Thank you for your feedback!

Sorry about that

How can we improve it?