Betrag einer komplexen Zahl
Berechnung des Absolutwerts und geometrische Interpretation
Der Betrag einer komplexen Zahl ist ein wichtiges Konzept, das die "Größe" oder "Entfernung vom Ursprung" in der Gauß'schen Zahlenebene beschreibt. Er gibt die Länge des Vektors an, der die komplexe Zahl darstellt.
Der Betrag wird auch als Absolutwert oder Modulus bezeichnet und ist immer eine nicht-negative reelle Zahl.
Grundlagen des Betrags
In der Gauß'schen Zahlenebene wird jede komplexe Zahl z = a + bi als Punkt oder Vektor dargestellt:
- Realteil a entspricht der x-Koordinate
- Imaginärteil b entspricht der y-Koordinate
- Der Vektor geht vom Ursprung (0, 0) zu dem Punkt (a, b)
Geometrische Darstellung
Bei der Darstellung mittels Ortsvektoren entsteht immer ein rechtwinkliges Dreieck:
- Katheten: Die Komponenten a und b
- Hypotenuse: Der Vektor z (von Ursprung zum Punkt)
- Länge der Hypotenuse: Der Betrag |z|
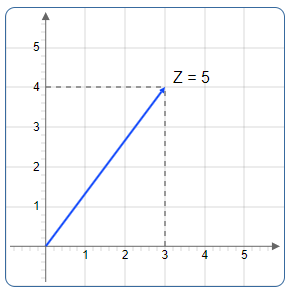
Graphik: Die komplexe Zahl 3 + 4i in der Gauß'schen Ebene
Definition und Formeln
|z| = √(a² + b²) = √(Re(z)² + Im(z)²)
Der Betrag wird mit dem Satz des Pythagoras berechnet, da die Komponenten a und b die Katheten eines rechtwinkligen Dreiecks bilden.
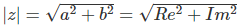
Alternative Berechnung mit der konjugierten Zahl
Es gibt auch eine alternative Formel, die die konjugierte komplexe Zahl nutzt:
|z| = √(z · z̄)
wobei z̄ die konjugierte komplexe Zahl ist (Imaginärteil hat umgekehrtes Vorzeichen)
Satz des Pythagoras
Direkter Zugang mit Realteil und Imaginärteil
Mit konjugierter Zahl
Elegant für theoretische Überlegungen
Beispiele zur Berechnung
Beispiel 1: Positive Real- und Imaginärteile
Berechnen Sie den Betrag der komplexen Zahl z = 3 + 4i
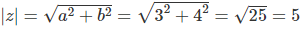
Beispiel 2: Negative Imaginärteile
Berechnen Sie den Betrag der komplexen Zahl z = 3 - 4i
Die komplexen Zahlen 3 + 4i und 3 - 4i haben den gleichen Betrag (beide 5), obwohl sie verschiedene Zahlen sind! Das liegt daran, dass sie den gleichen Abstand zum Ursprung haben.
Beispiel 3: Mit konjugierter Zahl
Berechnen Sie den Betrag von z = 3 - 4i mit der konjugierten Zahl
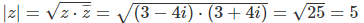
Weitere Beispiele
Verschiedene komplexe Zahlen
| Komplexe Zahl z | Realteil a | Imaginärteil b | Berechnung | Betrag |z| |
|---|---|---|---|---|
| 5 | 5 | 0 | √(5² + 0²) | 5 |
| 3i | 0 | 3 | √(0² + 3²) | 3 |
| 1 + i | 1 | 1 | √(1² + 1²) | √2 ≈ 1,41 |
| -2 + 3i | -2 | 3 | √(4 + 9) | √13 ≈ 3,61 |
| -1 - i | -1 | -1 | √(1 + 1) | √2 ≈ 1,41 |
Eigenschaften des Betrags
Nicht-negativität
|z| ≥ 0 für alle z ∈ ℂ
Der Betrag ist immer nicht-negativ
Null nur für Null
|z| = 0 ⟺ z = 0
Nur die Zahl 0 hat Betrag 0
Multiplikativität
|z₁ · z₂| = |z₁| · |z₂|
Betrag des Produkts = Produkt der Beträge
Division
|z₁/z₂| = |z₁|/|z₂|
Betrag des Quotienten = Quotient der Beträge
Dreiecksungleichung
|z₁ + z₂| ≤ |z₁| + |z₂|
Betrag der Summe ≤ Summe der Beträge
Mit konjugierter Zahl
|z|² = z · z̄
Quadrat des Betrags = z mal konjugiert
Praktische Anwendungen
Elektrotechnik und Physik
- Wechselstromkreise: Der Betrag der Impedanz bestimmt die Stromstärke
- Schwingungen: Amplitude von oszillierenden Systemen
- Wellenmechanik: Wahrscheinlichkeitsinterpretation in der Quantenmechanik
Mathematik und Signalverarbeitung
- Fourier-Analyse: Magnitude der Fourier-Koeffizienten
- Regelungstechnik: Stabilität von Systemen
- Fraktal-Geometrie: Bedingungen für Divergenz und Konvergenz
Vergleich: Betrag reeller und komplexer Zahlen
| Aspekt | Reelle Zahlen | Komplexe Zahlen |
|---|---|---|
| Darstellung | Zahlenstrahl (1D) | Gauß'sche Ebene (2D) |
| Betrag | |x| = Abstand zur 0 | |z| = Abstand zum Ursprung |
| Berechnung | |x| = Absolutwert | |z| = √(a² + b²) |
| Symmetrie | |x| = |-x| | |z| = |z̄| |
| Interpretation | Größe der Zahl | Entfernung vom Ursprung |
Tipps zum Verständnis und zur Berechnung
- Visualisieren Sie: Zeichnen Sie die komplexe Zahl in der Gauß'schen Ebene
- Nutzen Sie Pythagoras: Der Betrag folgt direkt aus dem Satz des Pythagoras
- Merken Sie sich Muster: z und z̄ haben den gleichen Betrag
- Praktizieren Sie: Berechnen Sie mehrere Beispiele selbst
- FALSCH: |a + bi| = |a| + |b| | RICHTIG: |a + bi| = √(a² + b²)
- FALSCH: |z| kann negativ sein | RICHTIG: |z| ≥ 0 immer
- FALSCH: |z₁ + z₂| = |z₁| + |z₂| | RICHTIG: |z₁ + z₂| ≤ |z₁| + |z₂|
Online-Tool
Teste deine Berechnungen mit unserem interaktiven Rechner:
Addition und Subtraktion
Multiplizieren
Konjugieren und Dividieren
Quadratische Gleichungen
Komplexe Zahlen geometrisch darstellen
Geometrische Addition
Betrag (Absoluter Wert)
Polarform
Polarform in Normalform umrechnen
Normalform in Polarform umrechnen
Multiplikation in Polarform
|
|