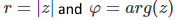Polar form of complex numbers
Description of the polar form of complex numbers
In the article on the geometric representation of complex numbers, it has been described that every complex number \(z\) in the Gaussian plane of numbers can be represented as a vector. This vector is uniquely determined by the real part and the imaginary part of the complex number \(z\).
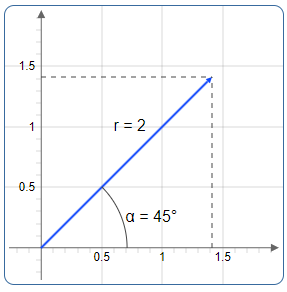
A vector emanating from the zero point can also be used as a pointer. This pointer is clearly defined by its length and the angle \(φ\) to the real axis.
The following figure shows the vector with the length \(r = 2\) and the angle \(φ = 45°\)
Positive angles are measured counterclockwise, negative angles are clockwise.
A complex number can thus be uniquely defined in the polar form by the pair \((|z|, φ)\). φ is the angle belonging to the vector. The length of the vector r corresponds to the absolute value \(|z|\) the complex number.
The general spelling is called normal form \(z = a + bi\)
We write in polar form
|
|