Geometric Addition and Subtraction of Complex Numbers
Understanding complex number operations as vector addition and subtraction in the Gaussian plane
Introduction to Geometric Operations
While complex number addition and subtraction are typically performed algebraically, they have beautiful geometric interpretations in the complex plane. Complex numbers can be represented as vectors, and their operations correspond to standard vector operations.
This geometric perspective provides intuitive understanding and connects complex algebra to vector geometry.
Every complex number \(z = a + bi\) can be represented as a vector from the origin to the point \((a, b)\). Addition and subtraction of complex numbers correspond to vector operations in the Gaussian plane.
Vector Representation of Complex Numbers
A complex number \(z = a + bi\) is uniquely determined by the ordered pair \((a, b)\). This pair corresponds to a vector in the complex plane:
The complex number \(z = a + bi\) is represented as:
- A point at coordinates \((a, b)\) in the complex plane
- A vector from the origin \(0\) to the point \((a, b)\)
- An arrow with starting point at origin and endpoint at \((a, b)\)
Vector Examples
- \(z = 3 + 2i\) represents the vector from \((0, 0)\) to \((3, 2)\)
- \(z = -1 + 4i\) represents the vector from \((0, 0)\) to \((-1, 4)\)
- \(z = 5\) represents the vector from \((0, 0)\) to \((5, 0)\)
- \(z = 3i\) represents the vector from \((0, 0)\) to \((0, 3)\)
Geometric Addition in the Complex Plane
When adding two complex numbers algebraically, we add real and imaginary parts separately. Geometrically, this corresponds to vector addition using the parallelogram method or triangle method.
The Addition Formula
For two complex numbers \(z_1 = a + bi\) and \(z_2 = c + di\):
\(\displaystyle z_1 + z_2 = (a + c) + (b + d)i\)
Adding two complex numbers geometrically means combining their vectors:
- Parallelogram Method: Place both vectors at the origin; the diagonal is the sum
- Triangle Method: Place the tail of the second vector at the head of the first
Example: Addition of \(z_1 = 3 + i\) and \(z_2 = 1 + 2i\)
Geometric Addition Example
Algebraic Calculation:
Geometric Interpretation:
- Vector \(z_1\) points from origin to \((3, 1)\)
- Vector \(z_2\) points from origin to \((1, 2)\)
- The sum \(z_1 + z_2\) points to \((4, 3)\)
Parallelogram Method:
Addition in the Complex Plane:
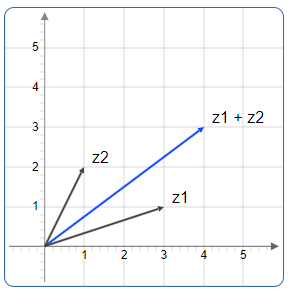
The diagonal of the parallelogram represents \(z_1 + z_2\)
Vector Addition Properties
Component-wise Addition
Real parts add to real partsImaginary parts add to imaginary parts
Commutativity
\(\displaystyle z_1 + z_2 = z_2 + z_1\)Order doesn't matter in addition
Associativity
\(\displaystyle (z_1 + z_2) + z_3 = z_1 + (z_2 + z_3)\)Grouping doesn't matter
Geometric Subtraction in the Complex Plane
Subtraction of complex numbers is closely related to addition. Geometrically, \(z_1 - z_2\) corresponds to adding the inverse vector of \(z_2\) to \(z_1\).
The Subtraction Formula
\(\displaystyle z_1 - z_2 = (a - c) + (b - d)i\)
Equivalent to Addition:
\(\displaystyle z_1 - z_2 = z_1 + (-z_2)\)
Subtracting two complex numbers geometrically means:
- Find the inverse vector \(-z_2\) (reflection through origin)
- Add \(z_1\) and \(-z_2\) using vector addition
- The result points from \(z_2\) to \(z_1\)
Example: Subtraction in the Complex Plane
Geometric Subtraction Example
Algebraic Calculation:
Geometric Method:
- Vector \(z_1\) points from origin to \((3, 1)\)
- Vector \(-z_2\) points from origin to \((-1, -2)\)
- Adding these vectors gives \((2, -1)\) = \(2 - i\
Subtraction in the Complex Plane:
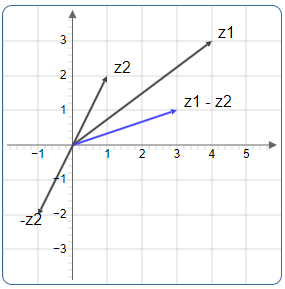
The vector from \(z_2\) to \(z_1\) represents \(z_1 - z_2\)
Two Equivalent Representations
The difference \(z_1 - z_2\) can be represented in two ways:
Vector from Origin
The vector from \((0, 0)\) to \(z_1 - z_2\)This is the standard representation
Vector Between Points
The vector from \(z_2\) to \(z_1\)Both vectors are equivalent (same length and direction)
Practical Insights
Why Geometric Representation Matters
Understanding complex operations geometrically helps us:
- Visualize complex number magnitudes and directions
- Understand rotation and scaling in the complex plane
- Solve practical problems in physics and engineering
- Gain intuition about complex number behavior
- Connect abstract algebra with spatial thinking
Connection to Vector Geometry
The geometric interpretation reveals that complex number operations follow the same rules as vector operations in 2D space. This connection is fundamental in:
- Physics: Representing forces, velocities, and accelerations
- Engineering: Signal processing and electrical circuits
- Computer Graphics: Transformations and rotations
- Quantum Mechanics: Wave functions and probability amplitudes
Summary of Geometric Operations
| Operation | Algebraic Form | Geometric Interpretation |
|---|---|---|
| Addition | \(\displaystyle (a+bi)+(c+di)\) | Vector addition (parallelogram or triangle method) |
| Subtraction | \(\displaystyle (a+bi)-(c+di)\) | Vector from \(z_2\) to \(z_1\), or \(z_1 + (-z_2)\) |
| Negation | \(\displaystyle -(a+bi) = -a-bi\) | Reflection through the origin (180° rotation) |
Key Points to Remember
- Complex numbers are vectors in the Gaussian plane
- Addition combines vectors using the parallelogram method
- Subtraction can be viewed as adding the inverse vector
- The difference \(z_1 - z_2\) is the vector from \(z_2\) to \(z_1\)
- Vector length equals the modulus \(|z|\)
- Vector direction is determined by the argument (angle)
|
|