Multiplication and Division in Polar Form

Simplifying complex arithmetic using polar coordinates

Introduction

One of the major advantages of the polar form representation is that multiplication and division become much simpler than in normal form. Instead of multiplying binomials, we only need to multiply magnitudes and add angles.

This geometric interpretation makes these operations intuitive and computationally efficient.

Key Advantage:

Polar form transforms complex multiplication into simple magnitude multiplication and angle addition—operations that are far easier to perform and understand geometrically.

Multiplication of Complex Numbers

The Multiplication Rule

When multiplying two complex numbers in polar form, we:

  • Multiply the magnitudes: \(r_1 \cdot r_2\)
  • Add the arguments: \(\varphi_1 + \varphi_2\)
Multiplication Formula:

For two complex numbers in polar form:

Polar Multiplication:
\(\displaystyle z_1 \cdot z_2 = r_1(\cos\varphi_1 + i\sin\varphi_1) \cdot r_2(\cos\varphi_2 + i\sin\varphi_2)\)

\(\displaystyle = r_1 r_2[\cos(\varphi_1 + \varphi_2) + i\sin(\varphi_1 + \varphi_2)]\)
Compact Notation:

\(\displaystyle |z_1 \cdot z_2| = |z_1| \cdot |z_2|\)   and   \(\arg(z_1 \cdot z_2) = \arg(z_1) + \arg(z_2)\)

Geometric Interpretation

Geometrically, multiplication in the complex plane corresponds to:

  • Scaling the first vector by the magnitude of the second
  • Rotating the first vector by the angle of the second

Geometric Multiplication in Polar Form:

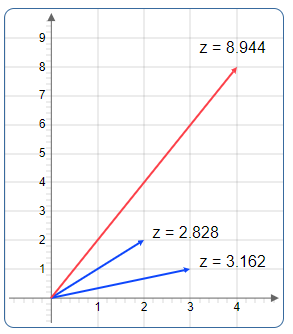
Geometric multiplication of complex numbers in polar form

The resulting vector has magnitude \(r_1 \cdot r_2\) and angle \(\varphi_1 + \varphi_2\)

Multiplication Examples

Example 1: Simple Angles

Multiply \(z_1 = 2(\cos 30° + i\sin 30°)\) and \(z_2 = 3(\cos 45° + i\sin 45°)\)

Step 1: Identify magnitudes and arguments

  • \(r_1 = 2\), \(\varphi_1 = 30°\)
  • \(r_2 = 3\), \(\varphi_2 = 45°\)

Step 2: Multiply magnitudes

\(\displaystyle r = r_1 \cdot r_2 = 2 \cdot 3 = 6\)

Step 3: Add arguments

\(\displaystyle \varphi = \varphi_1 + \varphi_2 = 30° + 45° = 75°\)

Result: \(z_1 \cdot z_2 = 6(\cos 75° + i\sin 75°)\)

Example 2: Right Angles

Multiply \(z_1 = 2(\cos 0° + i\sin 0°) = 2\) and \(z_2 = 3(\cos 90° + i\sin 90°) = 3i\)

Polar multiplication:

\(\displaystyle r = 2 \cdot 3 = 6\)
\(\displaystyle \varphi = 0° + 90° = 90°\)

Result: \(z_1 \cdot z_2 = 6(\cos 90° + i\sin 90°) = 6i\)

Verification (normal form): \(2 \cdot 3i = 6i\) ✓

Division of Complex Numbers

The Division Rule

Division in polar form is equally elegant. When dividing, we:

  • Divide the magnitudes: \(\frac{r_1}{r_2}\)
  • Subtract the arguments: \(\varphi_1 - \varphi_2\)
Division Formula:

For two complex numbers in polar form (with \(z_2 \neq 0\)):

Polar Division:
\(\displaystyle \frac{z_1}{z_2} = \frac{r_1(\cos\varphi_1 + i\sin\varphi_1)}{r_2(\cos\varphi_2 + i\sin\varphi_2)}\)

\(\displaystyle = \frac{r_1}{r_2}[\cos(\varphi_1 - \varphi_2) + i\sin(\varphi_1 - \varphi_2)]\)
Compact Notation:

\(\displaystyle \left|\frac{z_1}{z_2}\right| = \frac{|z_1|}{|z_2|}\)   and   \(\arg\left(\frac{z_1}{z_2}\right) = \arg(z_1) - \arg(z_2)\)

Division Examples

Example 1: Simple Angles

Divide \(z_1 = 8(\cos 120° + i\sin 120°)\) by \(z_2 = 2(\cos 30° + i\sin 30°)\)

Step 1: Identify magnitudes and arguments

  • \(r_1 = 8\), \(\varphi_1 = 120°\)
  • \(r_2 = 2\), \(\varphi_2 = 30°\)

Step 2: Divide magnitudes

\(\displaystyle r = \frac{r_1}{r_2} = \frac{8}{2} = 4\)

Step 3: Subtract arguments

\(\displaystyle \varphi = \varphi_1 - \varphi_2 = 120° - 30° = 90°\)

Result: \(\displaystyle \frac{z_1}{z_2} = 4(\cos 90° + i\sin 90°) = 4i\)

Example 2: Equal Magnitudes

Divide \(z_1 = 5(\cos 60° + i\sin 60°)\) by \(z_2 = 5(\cos 15° + i\sin 15°)\)

Polar division:

\(\displaystyle r = \frac{5}{5} = 1\)
\(\displaystyle \varphi = 60° - 15° = 45°\)

Result: \(\displaystyle \frac{z_1}{z_2} = 1(\cos 45° + i\sin 45°) = \frac{\sqrt{2}}{2} + i\frac{\sqrt{2}}{2}\)

Multiplication and Division Summary

Operation Normal Form Polar Form Computational Complexity
Multiplication Complex (FOIL) Multiply \(r\), add \(\varphi\) Much simpler
Division Complex (rationalize) Divide \(r\), subtract \(\varphi\) Much simpler
Powers Very complex De Moivre: \(r^n\), multiply \(\varphi\) by \(n\) Extremely simple

Advantages of Polar Form Operations

Speed
Simple arithmetic operations
No binomial expansion needed
Geometric Insight
Clear geometric meaning
Scaling and rotation operations
Error Reduction
Fewer algebraic steps
Less chance for mistakes
Computer Efficiency
Faster computation
Better for numerical algorithms

Key Points to Remember

  • Multiplication: Multiply magnitudes, add arguments
  • Division: Divide magnitudes, subtract arguments
  • Formula for multiplication: \(z_1 \cdot z_2 = r_1 r_2[\cos(\varphi_1 + \varphi_2) + i\sin(\varphi_1 + \varphi_2)]\)
  • Formula for division: \(\displaystyle \frac{z_1}{z_2} = \frac{r_1}{r_2}[\cos(\varphi_1 - \varphi_2) + i\sin(\varphi_1 - \varphi_2)]\)
  • Polar form is much simpler for multiplication and division than normal form
  • This is one of the main reasons polar form is used in engineering and physics
  • Angles may need adjustment if result exceeds 360° or is negative
























Is this page helpful?            
Thank you for your feedback!

Sorry about that

How can we improve it?