Geometric Representation of Complex Numbers
Understanding complex numbers through the complex plane (Argand diagram)
Introduction to the Complex Plane
Complex numbers can be represented geometrically in a two-dimensional coordinate system called the complex plane or Argand diagram. This geometric representation provides valuable insights into complex number operations and relationships.
Since every complex number is uniquely determined by an ordered pair of real numbers \((a, b)\), we can visualize them as points in a plane, just like Cartesian coordinates.
The complex plane is named after Jean-Robert Argand, though it was also independently developed by Carl Friedrich Gauss and Caspar Wessel.
The Complex Plane Structure
The complex plane is a coordinate system with two perpendicular axes, similar to the Cartesian plane, but with special interpretations for the axes.
A complex number \(z = a + bi\) is represented as a point \((a, b)\) in the complex plane.
The Two Axes of the Complex Plane
Real Axis (Horizontal)
Represents the real part \(a\)Labeled as \(\mathbb{R}\) or \(\text{Re}\)
Unit: \(1\) to the right of origin
Imaginary Axis (Vertical)
Represents the imaginary part \(b\)Labeled as \(i\mathbb{R}\) or \(\text{Im}\)
Unit: \(i\) above origin
Origin (Zero Point)
The point \((0, 0)\)Represents the complex number \(0\)
Intersection of both axes
A complex number \(z = a + bi\) corresponds to the point with coordinates:
Examples: Plotting Complex Numbers
Example 1: Simple Complex Number
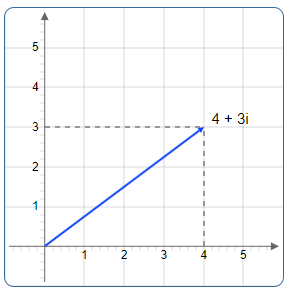
Plot \(z = 4 + 3i\)
- Real part: \(a = 4\) (move 4 units right on real axis)
- Imaginary part: \(b = 3\) (move 3 units up on imaginary axis)
- Point coordinates: \((4, 3)\)
Complex Plane Representation:
Example 2: Multiple Complex Numbers
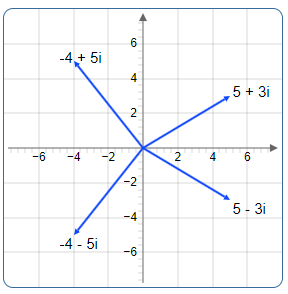
Plot Multiple Complex Numbers
- \(z_1 = -4 + 5i\) — 4 units left, 5 units up
- \(z_2 = -4 - 5i\) — 4 units left, 5 units down
- \(z_3 = 5 + 3i\) — 5 units right, 3 units up
- \(z_4 = 5 - 3i\) — 5 units right, 3 units down
Complex Plane with Multiple Points:
Geometric Transformations
Certain operations on complex numbers correspond to specific geometric transformations in the complex plane. Understanding these transformations provides geometric insight into complex arithmetic.
Negation: Reflection Through the Origin
The negation of a complex number \(-z\) corresponds to a point reflection (or 180° rotation) around the origin.
For \(z = a + bi\):
Example: Negation
- \(z = 3 + 2i \quad \Rightarrow \quad -z = -3 - 2i\)
- Graphically: rotate 180° around origin
Conjugation: Reflection Across the Real Axis
The complex conjugate \(\overline{z}\) corresponds to a reflection across the real axis.
For \(z = a + bi\):
Example: Conjugation
- \(z = 3 + 2i \quad \Rightarrow \quad \overline{z} = 3 - 2i\)
- Graphically: reflect across the real axis (horizontal)
Geometric Comparison
Transformations in the Complex Plane:
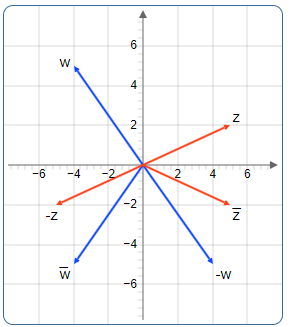
Showing a complex number \(z\), its negation \(-z\), and its conjugate \(\overline{z}\)
Properties of Geometric Representation
Symmetry in the Complex Plane
| Transformation | Geometric Operation | Algebraic Form | Example |
|---|---|---|---|
| Negation | 180° rotation around origin | \(-z = -a - bi\) \(-(3+2i) = -3-2i\) | |
| Conjugation | Reflection across real axis | \(\overline{z} = a - bi\) \(\overline{3+2i} = 3-2i\) | |
| Opposite Conjugate | Reflection across imaginary axis | \(-\overline{z} = -a + bi\) \(-(3-2i) = -3+2i\) |
Important Geometric Insights
Non-Real Complex Number Solutions to Quadratic Equations
If \(z\) is a non-real solution to a quadratic equation with real coefficients, then \(\overline{z}\) (the conjugate) is also a solution. Geometrically, this means that non-real solutions appear as symmetric pairs reflected across the real axis.
Example: Quadratic Equation Solutions
For the equation \(z^2 - 4z + 5 = 0\):
- Solutions: \(z_1 = 2 + i\) and \(z_2 = 2 - i\)
- These are complex conjugates of each other
- In the complex plane, they appear symmetric across the real axis
- Both are at distance 2 from the real axis
Distance from Origin: The Modulus
In the complex plane, the modulus (or absolute value) of a complex number represents the distance from the origin to the point representing that number.
For \(z = a + bi\), the modulus is:
Example: Calculate Modulus
For \(z = 3 + 4i\):
The point \((3, 4)\) is 5 units away from the origin.
Summary of Geometric Representation
Key Concepts:
- Complex numbers are represented as points in a 2D plane
- The horizontal axis represents the real part
- The vertical axis represents the imaginary part
- Negation corresponds to a 180° rotation around the origin
- Conjugation corresponds to reflection across the real axis
- The modulus represents the distance from the origin
- Complex conjugate solutions to real equations are symmetric
The geometric representation of complex numbers bridges algebra and geometry, allowing us to visualize complex operations and understand their behavior intuitively. This visualization is particularly useful for understanding multiplication, rotation, and complex transformations.
|
|