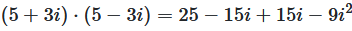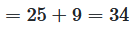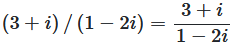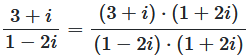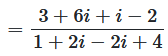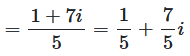Division of complex numbers
Description of how to conjugate and divide complex numbers
Conjugate complex numbers
Before we get to the division of complex numbers, we introduced a new concept. Every complex number has a so-called complex conjugate number. This conjugate complex number is needed here in the division, but we will come back to it later in other chapters.
As an example we take the number 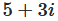 .
The complex number conjugated to
.
The complex number conjugated to 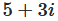 is
is 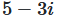 .
The real parts of the two numbers are the same, the imaginary parts of the two differ only by the sign.
.
The real parts of the two numbers are the same, the imaginary parts of the two differ only by the sign.
Let's take a look at the product of the two numbers
The product of the complex numbers and their conjugates is real. This is a special property of conjugate complex numbers that will prove useful again and again.
For the conjugate complex number 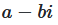 we write
we write 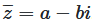 .
.
In the example above 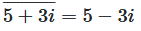
Division
Now let's talk about dividing complex numbers.
In the next example we will divide the number 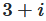 by the number
by the number 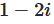 . We are looking for
. We are looking for
According to the principle of permanence, the calculation rules of the real numbers should be valid here. It bothers us that in the denominator of the break, the i occurs. Division by a real number would be very easy.
This is where the complex conjugate comes into play.
The fraction is extended by the conjugate complex number 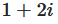 of the denominator.
This allows the \(i\) to be truncated in the denominator and the denominator becomes a real number.
Only in the numerator remains a complex number, which can be easily multiplied out.
of the denominator.
This allows the \(i\) to be truncated in the denominator and the denominator becomes a real number.
Only in the numerator remains a complex number, which can be easily multiplied out.
The division looks like this
The result is 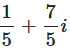
This article describes the division of complex numbers in normal form. Easier to calculate is the Division of complex numbers in polar form.
|
|