Konjugieren und Dividieren komplexer Zahlen
Konjugierte Zahlen und Division in Normalform und Polarform
Die konjugiert komplexe Zahl und die Division sind zwei wichtige Konzepte bei komplexen Zahlen. Die konjugierte Zahl wird nicht nur für die Division benötigt, sondern auch in vielen anderen Bereichen der Mathematik und Physik.
Konjugiert komplexe Zahlen
Jede komplexe Zahl besitzt eine konjugiert komplexe Zahl (oder kurz: Konjugierte). Sie entsteht, indem man das Vorzeichen des Imaginärteils umkehrt.
Ist z = a + bi, dann ist z̄ = a - bi
Die Konjugierte wird mit einem Strich über dem Symbol (z̄) oder manchmal als z* geschrieben.
Beispiele von konjugierten Zahlen
Verschiedene Paare
| Komplexe Zahl z | Konjugierte z̄ | Realteil | Imaginärteil ändert sich |
|---|---|---|---|
| 5 + 3i | 5 - 3i | Gleich (5) | 3 → -3 |
| 2 - 4i | 2 + 4i | Gleich (2) | -4 → 4 |
| -3 + 2i | -3 - 2i | Gleich (-3) | 2 → -2 |
| 6 (rein reell) | 6 | Gleich (6) | Keine Änderung |
| 3i (rein imaginär) | -3i | Gleich (0) | 3 → -3 |
Wichtige Eigenschaft: Produkt mit der Konjugierten
Eine besondere Eigenschaft: Das Produkt einer komplexen Zahl mit ihrer Konjugierten ist immer reell!
z · z̄ = (a + bi) · (a - bi) = a² + b² = |z|²
Das Ergebnis ist immer eine reelle Zahl und entspricht dem Quadrat des Betrags!
Beispiel: Produkt mit Konjugierter
Berechnen Sie (5 + 3i) · (5 - 3i)
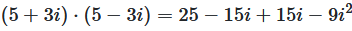
In der Gauß'schen Zahlenebene spiegelt die Konjugation eine komplexe Zahl an der reellen Achse (x-Achse). Der Betrag bleibt gleich, nur das Vorzeichen des Imaginärteils ändert sich.
Eigenschaften der Konjugierten
Doppelte Konjugation
z̄̄ = z
Die Konjugierte der Konjugierten ist wieder z
Addition
(z₁ + z₂)̄ = z̄₁ + z̄₂
Konjugation ist linear
Subtraktion
(z₁ - z₂)̄ = z̄₁ - z̄₂
Auch bei Subtraktion linear
Multiplikation
(z₁ · z₂)̄ = z̄₁ · z̄₂
Multiplikative Struktur erhalten
Division
(z₁/z₂)̄ = z̄₁/z̄₂
Auch bei Division erhalten
Betrag
|z̄| = |z|
Konjugierte hat gleichen Betrag
Division komplexer Zahlen
Die Division zweier komplexer Zahlen ist mit Hilfe der konjugierten Zahl elegant zu lösen. Der Trick: Wir erweitern den Bruch mit der Konjugierten des Nenners!
z₁/z₂ = (z₁ · z̄₂)/(z₂ · z̄₂) = (z₁ · z̄₂)/(a² + b²)
Die Erweiterung mit der Konjugierten des Nenners macht diesen zu einer reellen Zahl.
Beispiel 1: Division mit positiven Komponenten
Teilen Sie z₁ = 3 + i durch z₂ = 1 - 2i
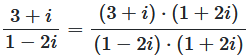
Beispiel 2: Mit negativen Komponenten
Teilen Sie z₁ = 2 - 3i durch z₂ = 1 + i
Beispiel 3: Spezialfall - Division durch rein imaginäre Zahl
Teilen Sie z₁ = 4 + 2i durch z₂ = 2i
Division in Polarform
Wie bei der Multiplikation ist die Division in Polarform deutlich einfacher!
z₁/z₂ = (r₁/r₂) · e^(i(φ₁ - φ₂))
In Worte: Beträge dividieren, Winkel subtrahieren!
- Betrag des Quotienten = Quotient der Beträge: |z₁/z₂| = |z₁| / |z₂|
- Winkel des Quotienten = Differenz der Winkel: arg(z₁/z₂) = arg(z₁) - arg(z₂)
- Geometrisch: Inverse Rotation und Skalierung
Übersicht: Divisionen
| z₁ | z₂ | z₁/z₂ | Schritte |
|---|---|---|---|
| 2 + 4i | 1 + i | 3 + i | Mit (1-i) erweitern |
| 5 | 2 - i | 2 + i | Mit (2+i) erweitern |
| 3i | 1 + 2i | -6/5 + 3i/5 | Mit (1-2i) erweitern |
| 1 + i | i | 1 - i | Mit (-i) erweitern |
Praktische Anwendungen
Elektrotechnik
- Impedanz: Z = U/I (Spannung durch Strom)
- Admittanz: Y = 1/Z (Kehrwert der Impedanz)
- Leistungsfaktor: cos(φ) bestimmt durch Division komplexer Größen
Signalverarbeitung
- Übertragungsfunktion: H(s) = Y(s)/X(s) (Ausgang/Eingang)
- Frequenzgang: H(jω) für verschiedene Frequenzen
Quantenmechanik
- Normalisierung: ⟨ψ|ψ⟩ mit konjugierter Wellenfunktion
- Erwartungswerte: ⟨ψ|Â|ψ⟩ mit Operatoren
Tipps und häufige Fehler
- Immer mit der Konjugierten erweitern: Das ist der Schlüssel!
- Nenner wird zu a² + b²: Eine reelle Zahl
- Zähler ausmultiplizieren: Dann Real- und Imaginärteil trennen
- Überprüfen mit Betrag: |z₁/z₂| = |z₁| / |z₂|
- In Polarform einfacher: Beträge dividieren, Winkel subtrahieren
- FALSCH: Nenner nicht ändern, wenn man mit Konjugierter erweitert | RICHTIG: Nenner wird zu a² + b²
- FALSCH: Vergessen, dass i² = -1 | RICHTIG: Immer ersetzen!
- FALSCH: Nur Realteile dividieren | RICHTIG: Kompletten Zähler und Nenner berechnen
- FALSCH: In Polarform: arg(z₁/z₂) = arg(z₁) / arg(z₂) | RICHTIG: = arg(z₁) - arg(z₂)
- FALSCH: Division durch 0 erlaubt | RICHTIG: z₂ ≠ 0 erforderlich!
Online-Tools
Teste deine Berechnungen mit unseren interaktiven Rechnern:
Addition und Subtraktion
Multiplizieren
Konjugieren und Dividieren
Quadratische Gleichungen
Komplexe Zahlen geometrisch darstellen
Geometrische Addition
Betrag (Absoluter Wert)
Polarform
Polarform in Normalform umrechnen
Normalform in Polarform umrechnen
Multiplikation in Polarform
|
|