Geometrische Addition und Subtraktion
Vektoraddition komplexer Zahlen in der Gaußschen Zahlenebene
Die Addition und Subtraktion komplexer Zahlen kann nicht nur algebraisch durchgeführt werden, sondern auch geometrisch visualisiert. Diese geometrische Perspektive entspricht der Vektoraddition in der Gaußschen Zahlenebene und bietet tiefere Einsicht in die Operationen.
Jede komplexe Zahl kann als Vektor vom Ursprung zu ihrem entsprechenden Punkt dargestellt werden.
Geometrische Addition
Das Konzept: Vektoraddition
Komplexe Zahlen werden algebraisch addiert, indem man Real- und Imaginärteile separat addiert:
z₁ + z₂ = (a₁ + bi₁) + (a₂ + b₂i) = (a₁ + a₂) + (b₁ + b₂)i
Dies ist identisch mit der Vektoraddition:
(a₁, b₁) + (a₂, b₂) = (a₁ + a₂, b₁ + b₂)

Geometrische Darstellung: Das Parallelogramm
In der Gaußschen Zahlenebene werden komplexe Zahlen als Vektoren dargestellt. Die Addition folgt der bekannten Vektoraddition:
Beispiel: z₁ = 3 + i und z₂ = 1 + 2i
- z₁ = 3 + i: Punkt (3, 1) in der Ebene
- z₂ = 1 + 2i: Punkt (1, 2) in der Ebene
- Summe: z₁ + z₂ = (3 + 1) + (1 + 2)i = 4 + 3i
- Ergebnis: Punkt (4, 3) in der Ebene
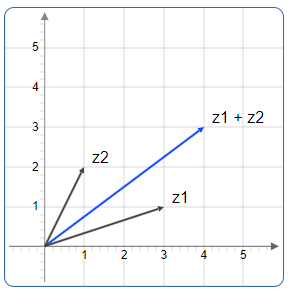
Abbildung 1: Vektoraddition von z₁ = 3 + i und z₂ = 1 + 2i. Der Vektor z₂ wird an z₁ angehängt.
Die Parallelogramm-Regel
Es gibt zwei äquivalente Möglichkeiten, die Addition geometrisch zu visualisieren:
Methode 1: Aneinanderhängen
Vektor z₂ wird an die Spitze von z₁ angehängt
Der Resultant-Vektor geht vom Ursprung zur finalen Spitze
Methode 2: Parallelogramm
Beide Vektoren mit gleichem Anfangspunkt bilden ein Parallelogramm
Die Diagonale des Parallelogramms ist die Summe
Beide Methoden führen zum gleichen Ergebnis! Die Wahl hängt davon ab, welche Darstellung am intuitivsten ist.
Geometrische Subtraktion
Das Konzept: Subtraktion als Addition der Negativen
Die Subtraktion wird geometrisch so durchgeführt, dass wir die Subtraktion in eine Addition umwandeln:
z₁ - z₂ = z₁ + (-z₂)
Wir addieren den Vektor -z₂ zum Vektor z₁
wobei -z₂ = -(a₂ + b₂i) = -a₂ - b₂i
Geometrische Darstellung der Subtraktion
Die Subtraktion z₁ - z₂ kann auf zwei äquivalente Weisen dargestellt werden:
Direkter Vektor
Der Vektor vom Ursprung zu (a₁ - a₂, b₁ - b₂)
Dies ist z₁ - z₂
Differenzvektor
Der Vektor von z₂ zu z₁
Beide Darstellungen sind identisch!
Beispiel: z₁ = 4 + 3i und z₂ = 1 + 2i
- z₁ = 4 + 3i: Punkt (4, 3) in der Ebene
- z₂ = 1 + 2i: Punkt (1, 2) in der Ebene
- -z₂ = -1 - 2i: Punkt (-1, -2) in der Ebene (Negation)
- Differenz: z₁ - z₂ = (4 - 1) + (3 - 2)i = 3 + i
- Resultat: Punkt (3, 1) in der Ebene
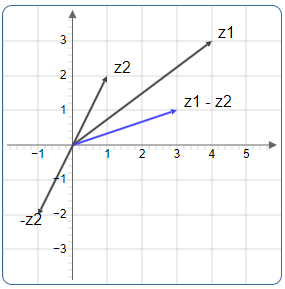
Abbildung 2: Geometrische Subtraktion. Der Differenzvektor kann vom Ursprung oder von z₂ zu z₁ gezeichnet werden.
Zwei Interpretationen der Differenz
Die Differenz z₁ - z₂ kann auf zwei Weisen geometrisch interpretiert werden:
| Interpretation | Darstellung | Vorteil |
|---|---|---|
| 1. Vektor vom Ursprung | Vektor von (0, 0) zu (a₁ - a₂, b₁ - b₂) | Zeigt die absolute Position des Ergebnisses |
| 2. Vektor zwischen Punkten | Vektor von z₂ zu z₁ | Zeigt die Verschiebung/Verbindung zwischen z₂ und z₁ |
Die beiden Vektoren sind identisch in Länge, Richtung und Orientierung. Je nachdem, was wir visualisieren möchten, können wir die eine oder andere Darstellung verwenden.
Eigenschaften der geometrischen Addition
Kommutativität
z₁ + z₂ = z₂ + z₁
Die Reihenfolge ist egal, das Parallelogramm bleibt gleich
Assoziativität
(z₁ + z₂) + z₃ = z₁ + (z₂ + z₃)
Vektoren können in beliebiger Reihenfolge angehängt werden
Längeneigenschaft
|z₁ + z₂| ≤ |z₁| + |z₂|
Dreiecksungleichung (kürzester Weg)
Null-Element
z + 0 = z
Addition mit der Null ändert nichts
Praktische Anwendungen
Elektrotechnik: Impedanzen
- Serienschaltung: Z_ges = Z₁ + Z₂ (Impedanzen addieren)
- Visualisierung: Vektoraddition von Impedanz und Reaktanz
Mechanik: Kraftvektoren
- Resultante: Gesamtkraft durch Vektoraddition
- Äquivalenz: Komplexe Zahlen ↔ 2D-Vektoren
Signalverarbeitung: Phasoren
- Überlagerung: Addition von Wellen/Signalen
- Geometrisch: Visualisierung der Phasenbeziehung
Zusammenfassung
| Operation | Algebraisch | Geometrisch |
|---|---|---|
| Addition | z₁ + z₂ = (a₁ + a₂) + (b₁ + b₂)i | Vektoraddition: Parallelogrammregel |
| Subtraktion | z₁ - z₂ = (a₁ - a₂) + (b₁ - b₂)i | Differenzvektor: Von z₂ zu z₁ |
| Negation | -z = -a - bi | Punktspiegelung am Ursprung |
| Länge | |z| = √(a² + b²) | Vektorlänge / Entfernung vom Ursprung |
Die geometrische Darstellung zeigt, dass komplexe Zahlen und Vektoren mathematisch äquivalent sind. Dies ermöglicht neue Perspektiven und macht viele Operationen intuitiver.
Addition und Subtraktion
Multiplizieren
Konjugieren und Dividieren
Quadratische Gleichungen
Komplexe Zahlen geometrisch darstellen
Geometrische Addition
Betrag (Absoluter Wert)
Polarform
Polarform in Normalform umrechnen
Normalform in Polarform umrechnen
Multiplikation in Polarform
|
|