Komplexe Zahlen geometrisch darstellen
Die Gaußsche Zahlenebene und ihre Interpretationen
Mit komplexen Zahlen lassen sich Operationen auch geometrisch darstellen. Die geometrische Darstellung eröffnet neue Perspektiven und ermöglicht es, tiefere mathematische Zusammenhänge zu verstehen.
Ein Bild sagt mehr als tausend Worte - und in der komplexen Mathematik oft auch mehr als tausend Gleichungen!
Die Gaußsche Zahlenebene
Komplexe Zahlen sind als z = a + bi definiert, wobei a und b reelle Zahlen sind. Jede komplexe Zahl ist also durch ein Zahlenpaar (a, b) eindeutig bestimmt.
Diese Eigenschaft ermöglicht die geometrische Darstellung komplexer Zahlen in einer 2D-Ebene, ähnlich wie Punkte in einem kartesischen Koordinatensystem.
Die Achsen der Gaußschen Ebene
Reelle Achse (Re oder ℝ)
Die horizontale x-Achse
Repräsentiert den Realteil a der komplexen Zahl
Die Zahl 1 liegt eine Einheit rechts vom Ursprung
Imaginäre Achse (Im oder iℝ)
Die vertikale y-Achse
Repräsentiert den Imaginärteil b der komplexen Zahl
Die Zahl i liegt eine Einheit oberhalb des Ursprungs
Eine komplexe Zahl z = a + bi wird als Punkt (a, b) in der Gaußschen Zahlenebene dargestellt:
- Die x-Koordinate ist der Realteil a
- Die y-Koordinate ist der Imaginärteil b
- Der Ursprung (0, 0) ist der Nullpunkt
Beispiele in der Gaußschen Ebene
Beispiel 1: Die komplexe Zahl 4 + 3i
Komponenten:
- Realteil: a = 4
- Imaginärteil: b = 3
- Darstellung: Punkt (4, 3)
- Position: 4 Einheiten rechts, 3 Einheiten oben vom Ursprung
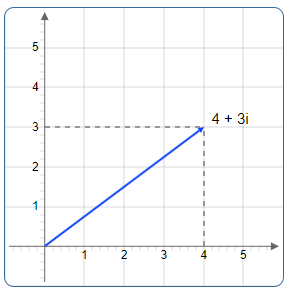
Abbildung 1: Die komplexe Zahl 4 + 3i als Punkt in der Gaußschen Zahlenebene
Beispiel 2: Mehrere komplexe Zahlen
Die folgende Abbildung zeigt mehrere komplexe Zahlen gleichzeitig:
Dargestellte Zahlen:
- -4 + 5i: Links oben (Realteil negativ, Imaginärteil positiv)
- -4 - 5i: Links unten (beide Komponenten negativ)
- 5 + 3i: Rechts oben (beide Komponenten positiv)
- 5 - 3i: Rechts unten (Realteil positiv, Imaginärteil negativ)
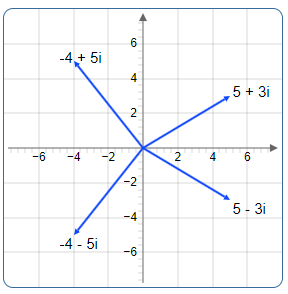
Abbildung 2: Mehrere komplexe Zahlen in verschiedenen Quadranten
Geometrische Transformationen
In der Gaußschen Zahlenebene entsprechen verschiedene mathematische Operationen geometrischen Transformationen (Spiegelungen, Drehungen, etc.).
1. Die Negative Zahl (-z): Punktspiegelung am Ursprung
Wenn z = a + bi, dann -z = -a - bi
Geometrisch: Der Punkt wird durch eine Punktspiegelung am Nullpunkt auf die gegenüberliegende Seite gespiegelt.
Beispiel:
- z = 3 + 2i liegt bei (3, 2)
- -z = -3 - 2i liegt bei (-3, -2)
- Die beiden Punkte sind diametral entgegengesetzt zum Ursprung
2. Die konjugierte Zahl (z̄): Achsenspiegelung an der reellen Achse
Wenn z = a + bi, dann z̄ = a - bi
Geometrisch: Der Punkt wird an der reellen Achse (x-Achse) gespiegelt. Der Realteil bleibt gleich, der Imaginärteil wechselt das Vorzeichen.
Beispiel:
- z = 3 + 2i liegt bei (3, 2)
- z̄ = 3 - 2i liegt bei (3, -2)
- Sie sind Spiegelbilder bezüglich der x-Achse
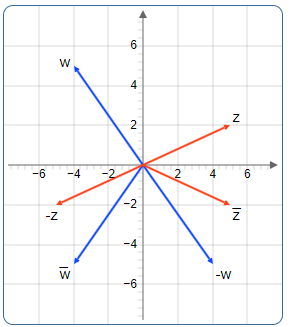
Abbildung 3: Geometrische Transformationen: -z (Punktspiegelung) und z̄ (Achsenspiegelung)
Die vier Quadranten
Die Gaußsche Zahlenebene wird durch die beiden Achsen in vier Quadranten eingeteilt:
| Quadrant | Realteil a | Imaginärteil b | Beispiel |
|---|---|---|---|
| I (oben rechts) | a > 0 | b > 0 | 3 + 2i |
| II (oben links) | a < 0 | b > 0 | -2 + 4i |
| III (unten links) | a < 0 | b < 0 | -3 - 5i |
| IV (unten rechts) | a > 0 | b < 0 | 4 - 2i |
Betrag und Argument in der Gaußschen Ebene
Der Betrag |z|: Die Entfernung vom Ursprung
Der Betrag einer komplexen Zahl z = a + bi ist die Distanz vom Ursprung zum Punkt (a, b).
|z| = √(a² + b²)
Dies ist die Länge des Vektors vom Ursprung zu z (Hypotenuse eines rechtwinkligen Dreiecks).
Das Argument arg(z): Der Winkel zur reellen Achse
Das Argument ist der Winkel φ, den der Vektor von z mit der positiven reellen Achse einschließt.
tan(φ) = b/a (mit Beachtung des Quadranten)
Der Winkel wird oft in Grad oder Radiant angegeben.
Beispiel: z = 3 + 3i
- Betrag: |z| = √(3² + 3²) = √18 ≈ 4,24
- Argument: tan(φ) = 3/3 = 1 → φ = 45° = π/4 rad
- Geometrisch: Punkt liegt 4,24 Einheiten vom Ursprung entfernt, unter 45° Winkel
Konjugierte Lösungen von quadratischen Gleichungen
Eine wichtige Eigenschaft: Wenn eine nicht-reelle Zahl z eine Lösung einer quadratischen Gleichung mit reellen Koeffizienten ist, dann ist auch die konjugierte Zahl z̄ eine Lösung.
Wenn az² + bz + c = 0 mit reellen a, b, c, dann erfüllt auch die konjugierte Zahl diese Gleichung:
a(z̄)² + b(z̄) + c = 0
Geometrisch: Die Lösungen liegen symmetrisch bezüglich der reellen Achse!
Beispiel: z² + 2z + 5 = 0
- Lösung 1: z₁ = -1 + 2i liegt bei (-1, 2)
- Lösung 2: z₂ = -1 - 2i liegt bei (-1, -2)
- Sie sind Spiegelbilder an der reellen Achse
- Beide haben den gleichen Realteil (-1)
Zusammenfassung: Geometrische Operationen
| Operation | Mathematisch | Geometrisch |
|---|---|---|
| Negative Zahl | z = a + bi → -z = -a - bi | Punktspiegelung am Ursprung (0, 0) |
| Konjugierte | z = a + bi → z̄ = a - bi | Achsenspiegelung an der reellen Achse |
| Betrag | |z| = √(a² + b²) | Entfernung vom Ursprung (Abstand) |
| Argument | arg(z) = arctan(b/a) | Winkel zur positiven reellen Achse |
Vorteile der geometrischen Darstellung
- Veranschaulichung: Komplexe Zahlen werden konkreter und verständlicher
- Symmetrien erkennen: Konjugierte und negative Zahlen zeigen symmetrische Muster
- Operationen verstehen: Addition wird zur Vektoraddition, Multiplikation zu Drehung und Skalierung
- Lösungen visualisieren: Lösungen von Gleichungen können grafisch dargestellt werden
- Geometrische Intuition: Verbindung zwischen Algebra und Geometrie
Addition und Subtraktion
Multiplizieren
Konjugieren und Dividieren
Quadratische Gleichungen
Komplexe Zahlen geometrisch darstellen
Geometrische Addition
Betrag (Absoluter Wert)
Polarform
Polarform in Normalform umrechnen
Normalform in Polarform umrechnen
Multiplikation in Polarform
|
|