Umwandlung: Polarform → Normalform

Vom Polar- zum kartesischen Koordinatensystem mit Trigonometrie

Die Umwandlung von Polarform (z = r·e^(iφ)) zur Normalform (z = a + bi) ist einfacher als die Umkehrung. Mit Hilfe der trigonometrischen Funktionen Cosinus und Sinus können wir Betrag und Winkel direkt in Real- und Imaginärteil umrechnen.

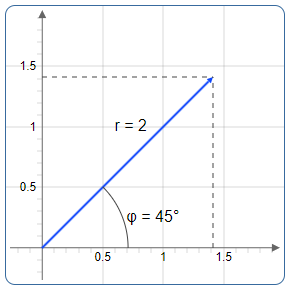
Bei der geometrischen Darstellung entsteht immer ein rechtwinkliges Dreieck, das wir zur Berechnung nutzen können.

Geometrische Grundlagen

In der Gaußschen Zahlenebene bildet ein Vektor mit den Koordinatenachsen immer ein rechtwinkliges Dreieck.

Die Komponenten:
  • Hypotenuse: Der Betrag r (Länge des Vektors)
  • Ankathete: Der Realteil a (horizontal)
  • Gegenkathete: Der Imaginärteil b (vertikal)
  • Winkel: Das Argument φ (zwischen Vektor und x-Achse)
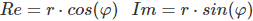
Rechtwinkliges Dreieck in der Gaußschen Ebene

Abbildung 1: Rechtwinkeliges Dreieck mit Sinus und Cosinus

Die Umwandlungsformeln

Mit Hilfe der trigonometrischen Funktionen können wir direkt von Polar- zu Normalform übergehen:

Umwandlungsformeln:

a = r · cos(φ)
b = r · sin(φ)

Daraus ergibt sich die Normalform:

z = a + bi = r·cos(φ) + i·r·sin(φ)

Trigonometrische Zerlegung
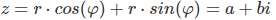
Umwandlung Polarform zu Normalform

Warum funktioniert das?

In einem rechtwinkligen Dreieck mit Hypotenuse r und Winkel φ gilt:

Trigonometrische Definition:
  • cos(φ) = Ankathete / Hypotenuse = a / r → a = r · cos(φ)
  • sin(φ) = Gegenkathete / Hypotenuse = b / r → b = r · sin(φ)

Praktische Beispiele

Beispiel 1: z = 2·e^(i·π/3) (60°)

Gegeben: z = 2·e^(i·π/3), also r = 2, φ = π/3 = 60°
Realteil berechnen: a = r · cos(φ) = 2 · cos(60°)
cos(60°) auswerten: cos(60°) = 1/2 = 0,5
Realteil: a = 2 · 0,5 = 1
Imaginärteil berechnen: b = r · sin(φ) = 2 · sin(60°)
sin(60°) auswerten: sin(60°) = √3/2 ≈ 0,866
Imaginärteil: b = 2 · (√3/2) = √3 ≈ 1,732
Normalform: z = 1 + √3·i ≈ 1 + 1,732i

Beispiel 2: z = 5·e^(i·53,13°)

Gegeben: z = 5·e^(i·53,13°), also r = 5, φ = 53,13°
Realteil berechnen: a = r · cos(φ) = 5 · cos(53,13°)
Taschenrechner: cos(53,13°) ≈ 0,6
Realteil: a = 5 · 0,6 = 3
Imaginärteil berechnen: b = r · sin(φ) = 5 · sin(53,13°)
Taschenrechner: sin(53,13°) ≈ 0,8
Imaginärteil: b = 5 · 0,8 = 4
Normalform: z = 3 + 4i

Beispiel 3: z = 4·e^(i·225°)

Gegeben: z = 4·e^(i·225°), also r = 4, φ = 225°
Realteil berechnen: a = r · cos(φ) = 4 · cos(225°)
Cosinus auswerten: cos(225°) = -√2/2 ≈ -0,707
Realteil: a = 4 · (-√2/2) = -2√2 ≈ -2,828
Imaginärteil berechnen: b = r · sin(φ) = 4 · sin(225°)
Sinus auswerten: sin(225°) = -√2/2 ≈ -0,707
Imaginärteil: b = 4 · (-√2/2) = -2√2 ≈ -2,828
Normalform: z = -2√2 - 2√2·i ≈ -2,828 - 2,828i

Spezielle Winkel und ihre Werte

Für häufig vorkommende Winkel sind die Werte von Sinus und Cosinus oft bekannt:

Winkel (Grad) Winkel (Radiant) cos(φ) sin(φ)
0° 0 1 0
30° π/6 √3/2 ≈ 0,866 1/2 = 0,5
45° π/4 √2/2 ≈ 0,707 √2/2 ≈ 0,707
60° π/3 1/2 = 0,5 √3/2 ≈ 0,866
90° π/2 0 1
180° π -1 0
270° 3π/2 0 -1
Tipp:

Diese speziellen Winkel treten häufig auf. Es lohnt sich, ihre Werte zu merken!

Übersicht aller Beispiele

Polarform Betrag r Winkel φ Realteil a Imaginärteil b Normalform
2·e^(i·π/3) 2 60° 2·cos(60°) = 1 2·sin(60°) = √3 1 + √3·i
5·e^(i·53,13°) 5 53,13° 5·cos(53,13°) = 3 5·sin(53,13°) = 4 3 + 4i
4·e^(i·225°) 4 225° 4·cos(225°) = -2√2 4·sin(225°) = -2√2 -2√2 - 2√2·i

Schritt-für-Schritt Anleitung

  1. Betrag und Winkel ablesen: Aus z = r·e^(iφ) die Werte für r und φ notieren
  2. Winkelmaß überprüfen: Ist φ in Grad oder Radiant? Taschenrechner einstellen!
  3. Cosinus berechnen: a = r · cos(φ)
  4. Sinus berechnen: b = r · sin(φ)
  5. Normalform schreiben: z = a + bi

Vergleich: Beide Richtungen

Normalform → Polarform

Gegeben: z = a + bi
Berechne:

r = √(a² + b²)
φ = arctan(b/a)

Polarform → Normalform

Gegeben: z = r·e^(iφ)
Berechne:

a = r·cos(φ)
b = r·sin(φ)

Wichtig:

Die Umwandlung von Polarform zu Normalform ist einfacher, da wir nur Sinus und Cosinus verwenden müssen. Rückwärts müssen wir Arcustangens verwenden und den Quadranten beachten!

Tipps und häufige Fehler

Praktische Tipps:
  • Taschenrechner richtig einstellen: DEG für Grad oder RAD für Radiant
  • Spezielle Winkel auswendig lernen: 30°, 45°, 60°, 90° für schnellere Berechnung
  • Größenordnung überprüfen: |a| ≤ r und |b| ≤ r müssen immer gelten
  • Vorzeichen beachten: Winkel > 90° führen zu negativen Komponenten
  • Verifikation: Betrag des Ergebnisses sollte gleich r sein
Häufige Fehler:
  • FALSCH: Winkelmaß verwechselt | RICHTIG: Taschenrechner korrekt einstellen
  • FALSCH: a = r·sin(φ), b = r·cos(φ) | RICHTIG: a = r·cos(φ), b = r·sin(φ)
  • FALSCH: Komponenten größer als Betrag | RICHTIG: |a|, |b| ≤ r
  • FALSCH: Winkel in Radiant, aber Taschenrechner auf Grad | RICHTIG: Maße konsistent halten

Online-Tool

Teste deine Umwandlungen mit unserem interaktiven Rechner:

























Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?